《2025年中学生世界七年级数学上册沪教版五四制》

13. 若$x+y= 3且xy= 1$,则代数式$(2-x)(2-y)$的值等于-1.

答案： 【解析】：
本题主要考察代数式的代入和计算。
首先，我们将代数式$(2-x)(2-y)$展开，得到：
$(2-x)(2-y) = 4 - 2y - 2x + xy$
然后，我们将$x+y=3$和$xy=1$代入上式，得到：
$(2-x)(2-y) = 4 - 2(x+y) + xy = 4 - 2 × 3 + 1 = -1$
【答案】：
$-1$

14. 若$a-b= 2$,则$2a^{2}-4ab+2b^{2}$的值为8.

答案： 【解析】：
本题主要考察代数式的因式分解和代入求值。
首先，我们将给定的代数式$2a^{2}-4ab+2b^{2}$进行因式分解。
观察该代数式，可以发现它是两个平方项的差的形式，且各项系数之间有一定的关系，即第一个和第三个项的系数都是2，第二个项的系数是-4，可以看作是-2的两倍。这提示我们可以尝试提取公因式，然后利用完全平方公式进行因式分解。
$2a^{2}-4ab+2b^{2}=2(a^{2}-2ab+b^{2})=2(a-b)^{2}$
然后，根据题目给出的条件$a-b=2$，我们可以将其代入到因式分解后的代数式中，得到：
$2(a-b)^{2}=2 × 2^{2}=8$
所以，$2a^{2}-4ab+2b^{2}$的值为8。
【答案】：
8

15. 计算：
(1)$(-\frac{1}{2}a^{2}b^{3})^{3}\cdot (-2a^{2}b)^{3}$； (2)$(a^{2})^{5}+(-a^{2}\cdot a^{3})^{2}+(-a^{2})^{5}-a\cdot a^{9}$；
(3)$2(x+1)+x(x+2)-(x-1)(x+5)$.

答案：
(1)解：原式$=(-\frac{1}{8}a^{6}b^{9})\cdot (-8a^{6}b^{3})$
$=(-\frac{1}{8})×(-8)\cdot a^{6+6}b^{9+3}$
$=1\cdot a^{12}b^{12}$
$=a^{12}b^{12}$
(2)解：原式$=a^{10}+(-a^{5})^{2}+(-a^{10})-a^{10}$
$=a^{10}+a^{10}-a^{10}-a^{10}$
$=0$
(3)解：原式$=2x + 2 + x^{2} + 2x - (x^{2} + 5x - x - 5)$
$=2x + 2 + x^{2} + 2x - x^{2} - 4x + 5$
$=(x^{2} - x^{2}) + (2x + 2x - 4x) + (2 + 5)$
$=0 + 0 + 7$
$=7$

16. 计算：
(1)$(a^{2}+a+1)(a^{2}-a+1)$； (2)$(2x-3y)(2x+3y)(4x^{2}+9y^{2})$.

答案：
(1)解：原式$=[(a^{2}+1)+a][(a^{2}+1)-a]$
$=(a^{2}+1)^{2}-a^{2}$
$=a^{4}+2a^{2}+1 - a^{2}$
$=a^{4}+a^{2}+1$
(2)解：原式$=[(2x)^{2}-(3y)^{2}](4x^{2}+9y^{2})$
$=(4x^{2}-9y^{2})(4x^{2}+9y^{2})$
$=(4x^{2})^{2}-(9y^{2})^{2}$
$=16x^{4}-81y^{4}$

17. 化简求值：$(x-y)^{2}-(2x+y)(x-3y)+(x+y)(x-y)$,其中$x= -1$,$y= 2$.

答案： 解：原式$=x^{2}-2xy+y^{2}-(2x^{2}-6xy+xy-3y^{2})+(x^{2}-y^{2})$
$=x^{2}-2xy+y^{2}-2x^{2}+5xy+3y^{2}+x^{2}-y^{2}$
$=3xy+3y^{2}$.
当$x=-1$，$y=2$时，
原式$=3×(-1)×2+3×2^{2}=-6+12=6$.

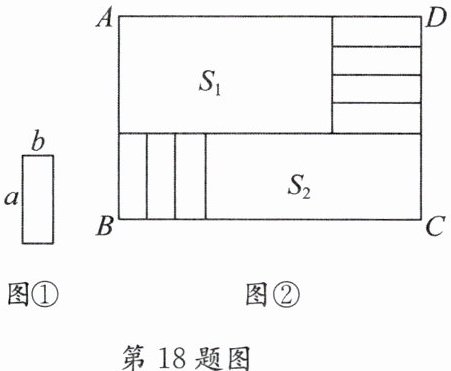
18. 将7张相同的小长方形纸片(如图①)按图②的方式不重叠地放在长方形$ABCD$内,未被覆盖的部分恰好被分割为两个长方形,面积分别记为$S_{1}$,$S_{2}$.已知小长方形纸片的长为$a$,宽为$b$,且$a＞b$,$AD= m$.
(1)当$AD= 20$时,用含$a$,$b的式子表示S_{1}$,$S_{2}$；
(2)若$AB$长度不变,$AD$变长,将这7张小长方形纸片还按照同样的方式放在新的长方形$ABCD$内,而$S_{1}-S_{2}$的值总保持不变,求$a$,$b$满足的数量关系.

答案：
(1)解：由图可知，$S_1$的长为$a$，宽为$AD - 3b$，$S_2$的长为$3b$，宽为$AD - a$。
当$AD = 20$时，
$S_1 = a(20 - 3b) = 20a - 3ab$，
$S_2 = 3b(20 - a) = 60b - 3ab$。
(2)解：设$AD = m$，则
$S_1 = a(m - 3b) = am - 3ab$，
$S_2 = 3b(m - a) = 3bm - 3ab$。
$S_1 - S_2 = (am - 3ab) - (3bm - 3ab) = (a - 3b)m$。
因为$S_1 - S_2$的值与$m$无关，所以$a - 3b = 0$，即$a = 3b$。
答：
(1)$S_1 = 20a - 3ab$，$S_2 = 60b - 3ab$；
(2)$a = 3b$。