《2025年阳光假日暑假六年级数学北师大版》

2. 某种电热壶的交易情况如下表。

(1)写出对应的总价与数量的比,求出比值,并比较大小。$120:1 = 120$，$240:2 = 120$，$360:3 = 120$，$480:4 = 120$，$1200:10 = 120$，比值相等。
(2)写出这个比值表示的实际意义。该种电热壶的单价。
(3)表中的数据能组成比例吗?为什么?如果能,请写出几个。能组成比例，因为总价与数量的比值（单价）一定。如$120:1 = 240:2$，$240:2 = 360:3$，$360:3 = 480:4$，$480:4 = 1200:10$（答案不唯一）。

答案： 【解析】：
(1) 计算总价与数量的比及比值：
$120:1 = 120÷1 = 120$；
$240:2 = 240÷2 = 120$；
$360:3 = 360÷3 = 120$；
$480:4 = 480÷4 = 120$；
$1200:10 = 1200÷10 = 120$。
这些比值相等。
(2) 这个比值表示的实际意义是该种电热壶的单价。
(3) 因为总价与数量的比值（单价）一定，所以表中的数据能组成比例。
例如：$120:1 = 240:2$；$240:2 = 360:3$；$360:3 = 480:4$；$480:4 = 1200:10$（答案不唯一）。
【答案】：
(1) $120:1 = 120$，$240:2 = 120$，$360:3 = 120$，$480:4 = 120$，$1200:10 = 120$，比值相等。
(2) 该种电热壶的单价。
(3) 能组成比例，因为总价与数量的比值（单价）一定。如$120:1 = 240:2$，$240:2 = 360:3$，$360:3 = 480:4$，$480:4 = 1200:10$（答案不唯一）。

3. 娟娟剪了两个正方形,它们的边长分别是4cm和8cm。请写出两个正方形的边长与边长、周长与周长、面积与面积的比,判断哪两个比能组成比例,并写出组成的比例。

答案： 【解析】：
1. 首先求边长比：
已知两个正方形边长分别为$a_1 = 4cm$，$a_2 = 8cm$，则边长比为$a_1:a_2=4:8 = 1:2$。
2. 然后求周长比：
根据正方形周长公式$C = 4a$，第一个正方形周长$C_1=4×4 = 16cm$，第二个正方形周长$C_2 = 4×8=32cm$，那么周长比$C_1:C_2=16:32 = 1:2$。
3. 接着求面积比：
根据正方形面积公式$S=a^2$，第一个正方形面积$S_1 = 4^2=16cm^2$，第二个正方形面积$S_2=8^2 = 64cm^2$，所以面积比$S_1:S_2=16:64 = 1:4$。
4. 最后判断比例：
判断两个比是否能组成比例，要看它们的比值是否相等。
因为边长比$4:8=\frac{1}{2}$，周长比$16:32=\frac{1}{2}$，面积比$16:64=\frac{1}{4}$，所以边长比和周长比的比值相等，能组成比例。
【答案】：边长比$4:8 = 1:2$；周长比$16:32 = 1:2$；面积比$16:64 = 1:4$；边长比和周长比能组成比例，组成的比例为$4:8 = 16:32$。

4. 小红说得对吗?

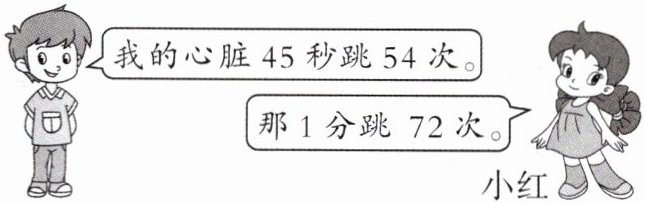
小红说得对

答案： 【解析】：
1. 首先统一单位：
因为$1$分$ = 60$秒。
已知$45$秒跳$54$次，先计算每秒跳的次数，根据除法的意义，每秒跳$54÷45=\frac{54}{45}=\frac{6}{5}$（次）。
再根据乘法的意义，计算$60$秒（$1$分）跳的次数，$\frac{6}{5}×60 = 6×12=72$（次）。
或者用比例的方法：设$1$分（$60$秒）跳$x$次，因为心跳次数和时间成正比例关系，则$\frac{54}{45}=\frac{x}{60}$。
根据比例的基本性质“内项之积等于外项之积”，可得$45x = 54×60$。
那么$x=\frac{54×60}{45}$，$54÷45 = 1.2$，$1.2×60 = 72$。
【答案】：小红说得对。