《2025年阳光假日暑假六年级数学北师大版》

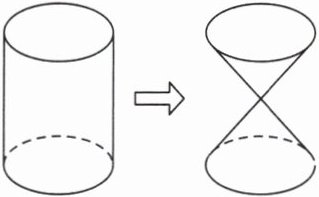
3. 如图所示,把一个体积是$24dm^{3}$的圆柱形木块削成由两个相对的圆锥组成的物体,每个圆锥的高是圆柱的一半,则每个圆锥的体积是4立方分米?

答案： 【解析】：
设圆柱的底面积为$S$，高为$h$，则圆柱体积$V = Sh = 24dm^{3}$。
每个圆锥的高是$\frac{h}{2}$，根据圆锥体积公式$V_{锥}=\frac{1}{3}Sh$，那么一个圆锥的体积$V_{1}=\frac{1}{3}S×\frac{h}{2}$。
因为$Sh = 24$，所以$V_{1}=\frac{1}{3}×\frac{1}{2}× Sh$，把$Sh = 24$代入可得$V_{1}=\frac{1}{3}×\frac{1}{2}×24$
$=\frac{1}{6}×24 = 4dm^{3}$。
【答案】：$4$

4. 从一个棱长为6 cm 的正方体的底面向内挖去一个最大的圆锥,剩下的立体图形的体积约是原正方体体积的百分之几？(百分号前保留一位小数)

答案： 【解析】：本题可先分别求出正方体的体积和圆锥的体积，再用正方体体积减去圆锥体积得到剩下立体图形的体积，最后计算剩下立体图形体积占原正方体体积的百分比。
**步骤一：计算正方体的体积**
根据正方体的体积公式$V=a^3$（其中$V$为正方体体积，$a$为正方体棱长），已知正方体棱长为$6cm$，可得正方体体积为：
$V_{正方体}=6^3 = 216cm^3$
**步骤二：计算圆锥的体积**
从正方体底面向内挖去一个最大的圆锥，这个圆锥的底面直径和高都等于正方体的棱长$6cm$。
根据圆锥的体积公式$V=\frac{1}{3}\pi r^2h$（其中$V$为圆锥体积，$r$为圆锥底面半径，$h$为圆锥的高），已知圆锥底面直径为$6cm$，则半径$r = 6÷2 = 3cm$，高$h = 6cm$，$\pi$取$3.14$，可得圆锥体积为：
$V_{圆锥}=\frac{1}{3}×3.14×3^2×6$
$=\frac{1}{3}×3.14×9×6$
$=3.14×3×6$
$=56.52cm^3$
**步骤三：计算剩下立体图形的体积**
剩下立体图形的体积等于正方体体积减去圆锥体积，即：
$V_{剩下}=V_{正方体}-V_{圆锥}=216 - 56.52 = 159.48cm^3$
**步骤四：计算剩下立体图形体积占原正方体体积的百分比**
用剩下立体图形的体积除以正方体体积再乘以$100\%$，可得：
$\frac{V_{剩下}}{V_{正方体}}×100\%=\frac{159.48}{216}×100\%\approx73.8\%$
【答案】：$73.8\%$

5. 一个近似于圆锥形状的野营帐篷,它的底面半径是3 m,高是2.4 m。

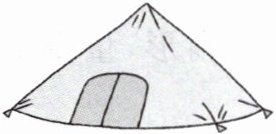
(1) 帐篷的占地面积是多少平方米? 28.26平方米
(2) 帐篷里面的空间有多大? 22.608立方米

答案： 【解析】：
(1) 求帐篷的占地面积，即求圆锥的底面积。根据圆的面积公式$S = \pi r^{2}$（其中$r$为半径，$\pi$取$3.14$），可得$3.14×3^{2}=3.14×9 = 28.26$（平方米）。
(2) 求帐篷里面的空间，即求圆锥的体积。根据圆锥体积公式$V=\frac{1}{3}Sh$（$S$是底面积，$h$是高），由
(1)知$S = 28.26$平方米，$h = 2.4$米，所以$\frac{1}{3}×28.26×2.4 = 28.26×0.8 = 22.608$（立方米）。
【答案】：
(1) $28.26$平方米
(2) $22.608$立方米