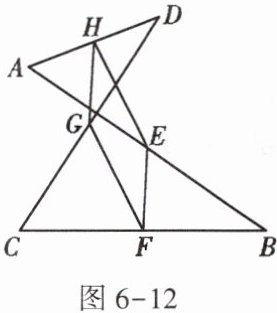
5. 如图6-12,E,F,G,H分别是线段AB,CB,CD,AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.

答案:
【解析】:连接$AC$。
因为$E$,$F$分别是线段$AB$,$CB$的中点,根据三角形中位线定理,所以$EF// AC$,$EF = \frac{1}{2}AC$。
因为$H$,$G$分别是线段$AD$,$CD$的中点,根据三角形中位线定理,所以$HG// AC$,$HG=\frac{1}{2}AC$。
所以$EF// HG$,$EF = HG$。
根据一组对边平行且相等的四边形是平行四边形,所以四边形$EFGH$是平行四边形。
【答案】:四边形$EFGH$是平行四边形。
因为$E$,$F$分别是线段$AB$,$CB$的中点,根据三角形中位线定理,所以$EF// AC$,$EF = \frac{1}{2}AC$。
因为$H$,$G$分别是线段$AD$,$CD$的中点,根据三角形中位线定理,所以$HG// AC$,$HG=\frac{1}{2}AC$。
所以$EF// HG$,$EF = HG$。
根据一组对边平行且相等的四边形是平行四边形,所以四边形$EFGH$是平行四边形。
【答案】:四边形$EFGH$是平行四边形。
1. 正九边形的一个内角的度数是()
A. $108^{\circ}$
B. $120^{\circ}$
C. $135^{\circ}$
D. $140^{\circ}$
A. $108^{\circ}$
B. $120^{\circ}$
C. $135^{\circ}$
D. $140^{\circ}$
答案:
D
2. 一个多边形的内角和是$900^{\circ}$,这个多边形的边数是______.
答案:
$7$
3. 若一个多边形的每一个外角都是$40^{\circ}$,则这个多边形是______.
答案:
九边形
4. 若一个多边形每一个内角都比与它相邻的外角大$90^{\circ}$,则这个多边形的边数是______.
答案:
$8$
5. 若一个多边形的内角和比四边形的内角和多$1080^{\circ}$,并且这个多边形的各内角都相等,则这个多边形的每个内角等于多少度?
答案:
【解析】:首先,根据多边形内角和公式$(n - 2)\times180^{\circ}$($n$为边数且$n\geqslant 3$且$n$为整数),四边形内角和为$(4 - 2)\times180^{\circ}=360^{\circ}$。
已知该多边形内角和比四边形内角和多$1080^{\circ}$,则这个多边形内角和为$360^{\circ}+1080^{\circ}=1440^{\circ}$。
设这个多边形的边数为$n$,可列方程$(n - 2)\times180^{\circ}=1440^{\circ}$,
解得$n - 2 = 1440^{\circ}\div180^{\circ}=8$,则$n = 8 + 2 = 10$,即这个多边形是十边形。
因为这个多边形各内角都相等,所以它的每个内角为$1440^{\circ}\div10 = 144^{\circ}$。
【答案】:$144^{\circ}$
已知该多边形内角和比四边形内角和多$1080^{\circ}$,则这个多边形内角和为$360^{\circ}+1080^{\circ}=1440^{\circ}$。
设这个多边形的边数为$n$,可列方程$(n - 2)\times180^{\circ}=1440^{\circ}$,
解得$n - 2 = 1440^{\circ}\div180^{\circ}=8$,则$n = 8 + 2 = 10$,即这个多边形是十边形。
因为这个多边形各内角都相等,所以它的每个内角为$1440^{\circ}\div10 = 144^{\circ}$。
【答案】:$144^{\circ}$
查看更多完整答案,请扫码查看


