6. 某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示,现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.
| |甲|乙|
|----|----|----|
|A|20克|40克|
|B|30克|20克|
设生产A种饮料x瓶,解答下列问题.
(1)有几种符合题意的生产方案?写出解答过程.
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低.
| |甲|乙|
|----|----|----|
|A|20克|40克|
|B|30克|20克|
设生产A种饮料x瓶,解答下列问题.
(1)有几种符合题意的生产方案?写出解答过程.
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低.
答案:
【解析】:
(1)
已知生产$A$种饮料$x$瓶,因为计划生产$A$,$B$两种饮料共$100$瓶,所以生产$B$种饮料$(100 - x)$瓶。
根据现用甲原料$2800$克,$A$饮料每瓶含甲原料$20$克,$B$饮料每瓶含甲原料$30$克,可得不等式$20x + 30(100 - x)\leq2800$;
根据现用乙原料$2800$克,$A$饮料每瓶含乙原料$40$克,$B$饮料每瓶含乙原料$20$克,可得不等式$40x+20(100 - x)\leq2800$。
解不等式$20x + 30(100 - x)\leq2800$:
$\begin{aligned}20x+3000 - 30x&\leq2800\\- 10x&\leq2800 - 3000\\-10x&\leq - 200\\x&\geq20\end{aligned}$
解不等式$40x + 20(100 - x)\leq2800$:
$\begin{aligned}40x+2000 - 20x&\leq2800\\20x&\leq2800 - 2000\\20x&\leq800\\x&\leq40\end{aligned}$
所以$x$的取值范围是$20\leq x\leq40$,因为$x$为瓶数,是正整数,所以$x$可以取$20$,$21$,$22$,$\cdots$,$40$,共$40 - 20+1 = 21$种符合题意的生产方案。
(2)
已知$A$种饮料每瓶的成本为$2.60$元,$B$种饮料每瓶的成本为$2.80$元,生产$A$种饮料$x$瓶,生产$B$种饮料$(100 - x)$瓶。
则成本总额$y = 2.6x+2.8(100 - x)$,化简可得:
$\begin{aligned}y&=2.6x + 280-2.8x\\y&=-0.2x + 280\end{aligned}$
因为$k=-0.2\lt0$,所以$y$随$x$的增大而减小,又因为$20\leq x\leq40$,所以当$x = 40$时,成本总额$y$最低。
【答案】:
(1)有$21$种符合题意的生产方案。过程:设生产$A$种饮料$x$瓶,则生产$B$种饮料$(100 - x)$瓶,根据甲、乙原料的用量列出不等式组$\begin{cases}20x + 30(100 - x)\leq2800\\40x+20(100 - x)\leq2800\end{cases}$,解得$20\leq x\leq40$,$x$为正整数,所以$x$有$21$个取值,即有$21$种生产方案。
(2)$y=-0.2x + 280$,当$x = 40$时,成本总额最低。
(1)
已知生产$A$种饮料$x$瓶,因为计划生产$A$,$B$两种饮料共$100$瓶,所以生产$B$种饮料$(100 - x)$瓶。
根据现用甲原料$2800$克,$A$饮料每瓶含甲原料$20$克,$B$饮料每瓶含甲原料$30$克,可得不等式$20x + 30(100 - x)\leq2800$;
根据现用乙原料$2800$克,$A$饮料每瓶含乙原料$40$克,$B$饮料每瓶含乙原料$20$克,可得不等式$40x+20(100 - x)\leq2800$。
解不等式$20x + 30(100 - x)\leq2800$:
$\begin{aligned}20x+3000 - 30x&\leq2800\\- 10x&\leq2800 - 3000\\-10x&\leq - 200\\x&\geq20\end{aligned}$
解不等式$40x + 20(100 - x)\leq2800$:
$\begin{aligned}40x+2000 - 20x&\leq2800\\20x&\leq2800 - 2000\\20x&\leq800\\x&\leq40\end{aligned}$
所以$x$的取值范围是$20\leq x\leq40$,因为$x$为瓶数,是正整数,所以$x$可以取$20$,$21$,$22$,$\cdots$,$40$,共$40 - 20+1 = 21$种符合题意的生产方案。
(2)
已知$A$种饮料每瓶的成本为$2.60$元,$B$种饮料每瓶的成本为$2.80$元,生产$A$种饮料$x$瓶,生产$B$种饮料$(100 - x)$瓶。
则成本总额$y = 2.6x+2.8(100 - x)$,化简可得:
$\begin{aligned}y&=2.6x + 280-2.8x\\y&=-0.2x + 280\end{aligned}$
因为$k=-0.2\lt0$,所以$y$随$x$的增大而减小,又因为$20\leq x\leq40$,所以当$x = 40$时,成本总额$y$最低。
【答案】:
(1)有$21$种符合题意的生产方案。过程:设生产$A$种饮料$x$瓶,则生产$B$种饮料$(100 - x)$瓶,根据甲、乙原料的用量列出不等式组$\begin{cases}20x + 30(100 - x)\leq2800\\40x+20(100 - x)\leq2800\end{cases}$,解得$20\leq x\leq40$,$x$为正整数,所以$x$有$21$个取值,即有$21$种生产方案。
(2)$y=-0.2x + 280$,当$x = 40$时,成本总额最低。
1. 若$m > n$,则下列不等式不一定成立的是( )
A. $m + 3 > n + 3$
B. $-3m < -3n$
C. $\frac{m}{3} > \frac{n}{3}$
D. $m^2 > n^2$
A. $m + 3 > n + 3$
B. $-3m < -3n$
C. $\frac{m}{3} > \frac{n}{3}$
D. $m^2 > n^2$
答案:
D
2. 在数轴上表示不等式$-2x ≤ 4$的解集,正确的是图2 - 3中的( )
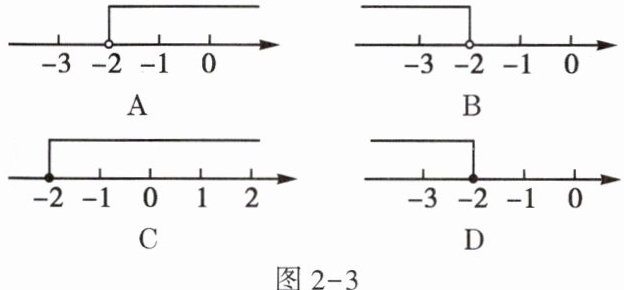

答案:
C
3. 如图2 - 4,当$y < 0$时,自变量x的取值范围是( )
A. $x < -2$
B. $x > -2$
C. $x < 2$
D. $x > 2$

A. $x < -2$
B. $x > -2$
C. $x < 2$
D. $x > 2$
答案:
D
4. 若关于x的一元一次方程$x - m + 2 = 0$的解是负数,则m的取值范围是( )
A. $m ≥ 2$
B. $m > 2$
C. $m < 2$
D. $m ≤ 2$
A. $m ≥ 2$
B. $m > 2$
C. $m < 2$
D. $m ≤ 2$
答案:
C
查看更多完整答案,请扫码查看


