6. 如图3-21,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为____.

答案:
1. 首先,明确旋转的性质:
设点$P(x,y)$绕原点$O$顺时针旋转$90^{\circ}$后得到点$P'(x',y')$。
对于点$(x,y)$绕原点顺时针旋转$90^{\circ}$的坐标变换公式为$\begin{cases}x' = y\\y'=-x\end{cases}$。
2. 然后,已知$P(2,3)$:
这里$x = 2$,$y = 3$。
根据上述公式,当$x = 2$,$y = 3$时,$x'=y = 3$,$y'=-x=-2$。
所以$P'$的坐标为$(3, - 2)$。
设点$P(x,y)$绕原点$O$顺时针旋转$90^{\circ}$后得到点$P'(x',y')$。
对于点$(x,y)$绕原点顺时针旋转$90^{\circ}$的坐标变换公式为$\begin{cases}x' = y\\y'=-x\end{cases}$。
2. 然后,已知$P(2,3)$:
这里$x = 2$,$y = 3$。
根据上述公式,当$x = 2$,$y = 3$时,$x'=y = 3$,$y'=-x=-2$。
所以$P'$的坐标为$(3, - 2)$。
7. 如图3-22,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC = 60°,则∠EFD的度数为____.


答案:
1. 首先,根据旋转的性质:
因为$\triangle BCE$绕点$C$顺时针方向旋转$90^{\circ}$得到$\triangle DCF$,所以$\triangle BCE\cong\triangle DCF$。
则$CE = CF$,$\angle BEC=\angle DFC = 60^{\circ}$,$\angle ECF = 90^{\circ}$。
2. 然后,在$\triangle ECF$中:
由于$CE = CF$,$\angle ECF = 90^{\circ}$,根据等腰直角三角形的性质,$\angle EFC=\angle FEC$。
根据三角形内角和定理$\angle EFC+\angle FEC+\angle ECF = 180^{\circ}$,设$\angle EFC=\angle FEC = x$,则$2x + 90^{\circ}=180^{\circ}$。
解方程$2x=180^{\circ}-90^{\circ}$,得$x = 45^{\circ}$,即$\angle EFC = 45^{\circ}$。
3. 最后,求$\angle EFD$的度数:
因为$\angle EFD=\angle DFC-\angle EFC$。
已知$\angle DFC = 60^{\circ}$,$\angle EFC = 45^{\circ}$,所以$\angle EFD=60^{\circ}-45^{\circ}=15^{\circ}$。
故答案为$15^{\circ}$。
因为$\triangle BCE$绕点$C$顺时针方向旋转$90^{\circ}$得到$\triangle DCF$,所以$\triangle BCE\cong\triangle DCF$。
则$CE = CF$,$\angle BEC=\angle DFC = 60^{\circ}$,$\angle ECF = 90^{\circ}$。
2. 然后,在$\triangle ECF$中:
由于$CE = CF$,$\angle ECF = 90^{\circ}$,根据等腰直角三角形的性质,$\angle EFC=\angle FEC$。
根据三角形内角和定理$\angle EFC+\angle FEC+\angle ECF = 180^{\circ}$,设$\angle EFC=\angle FEC = x$,则$2x + 90^{\circ}=180^{\circ}$。
解方程$2x=180^{\circ}-90^{\circ}$,得$x = 45^{\circ}$,即$\angle EFC = 45^{\circ}$。
3. 最后,求$\angle EFD$的度数:
因为$\angle EFD=\angle DFC-\angle EFC$。
已知$\angle DFC = 60^{\circ}$,$\angle EFC = 45^{\circ}$,所以$\angle EFD=60^{\circ}-45^{\circ}=15^{\circ}$。
故答案为$15^{\circ}$。
8. 边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为____cm.
答案:
1. 首先明确弧长公式:
弧长公式为$l = \frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角的度数,$r$为半径)。
2. 然后分析题目条件:
正方形$ABCD$绕顶点$A$旋转$180^{\circ}$,顶点$B$所经过的路线是以$A$为圆心,$AB$长为半径的一段弧。
已知正方形边长$AB = 4cm$,圆心角$n = 180^{\circ}$,半径$r=AB = 4cm$。
3. 最后代入弧长公式计算:
把$n = 180$,$r = 4$代入弧长公式$l=\frac{n\pi r}{180}$,可得$l=\frac{180\pi\times4}{180}$。
化简$\frac{180\pi\times4}{180}=4\pi(cm)$。
故顶点$B$所经过的路线长为$4\pi$ $cm$。
弧长公式为$l = \frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角的度数,$r$为半径)。
2. 然后分析题目条件:
正方形$ABCD$绕顶点$A$旋转$180^{\circ}$,顶点$B$所经过的路线是以$A$为圆心,$AB$长为半径的一段弧。
已知正方形边长$AB = 4cm$,圆心角$n = 180^{\circ}$,半径$r=AB = 4cm$。
3. 最后代入弧长公式计算:
把$n = 180$,$r = 4$代入弧长公式$l=\frac{n\pi r}{180}$,可得$l=\frac{180\pi\times4}{180}$。
化简$\frac{180\pi\times4}{180}=4\pi(cm)$。
故顶点$B$所经过的路线长为$4\pi$ $cm$。
9. 如图3-23,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为____cm.
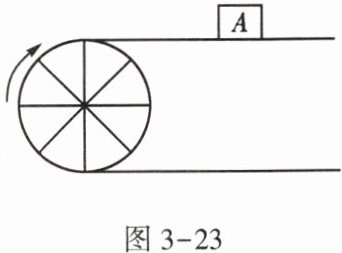

答案:
1. 首先明确弧长公式:
弧长公式为$l = \frac{n\pi r}{180}$(其中$n$是圆心角的度数,$r$是半径)。
2. 然后分析题目条件:
已知转动轮半径$r = 30cm$,转过的圆心角$n = 120^{\circ}$。
因为传送带上物体$A$平移的距离等于转动轮上对应弧长。
3. 最后计算弧长:
根据弧长公式$l=\frac{n\pi r}{180}$,将$n = 120$,$r = 30$代入公式。
则$l=\frac{120\times\pi\times30}{180}$。
先计算$\frac{120\times30}{180}=20$,所以$l = 20\pi$。
故传送带上的物体$A$平移的距离为$20\pi$ $cm$。
弧长公式为$l = \frac{n\pi r}{180}$(其中$n$是圆心角的度数,$r$是半径)。
2. 然后分析题目条件:
已知转动轮半径$r = 30cm$,转过的圆心角$n = 120^{\circ}$。
因为传送带上物体$A$平移的距离等于转动轮上对应弧长。
3. 最后计算弧长:
根据弧长公式$l=\frac{n\pi r}{180}$,将$n = 120$,$r = 30$代入公式。
则$l=\frac{120\times\pi\times30}{180}$。
先计算$\frac{120\times30}{180}=20$,所以$l = 20\pi$。
故传送带上的物体$A$平移的距离为$20\pi$ $cm$。
10. 如图3-24,P是等边三角形ABC内一点,PA = 6,PB = 8,PC = 10,则∠APB的度数为____.


答案:
1. 首先,将$\triangle APB$绕点$B$顺时针旋转$60^{\circ}$:
设旋转后$A$点与$C$点重合,$P$点旋转到$P'$点,连接$PP'$。
因为$\triangle ABC$是等边三角形,$\angle ABC = 60^{\circ}$,由旋转性质可知:$BP = BP'$,$\angle PBP'=60^{\circ}$,$AP = CP'=6$。
2. 然后,判断$\triangle BPP'$的形状:
在$\triangle BPP'$中,由于$BP = BP'$,$\angle PBP' = 60^{\circ}$,根据等边三角形的判定定理(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可得$\triangle BPP'$是等边三角形。
所以$PP'=BP = 8$,$\angle BP'P = 60^{\circ}$。
3. 接着,判断$\triangle PP'C$的形状:
在$\triangle PP'C$中,$PP' = 8$,$CP' = 6$,$PC = 10$。
根据勾股定理的逆定理$a^{2}+b^{2}=c^{2}$(其中$a = 6$,$b = 8$,$c = 10$),因为$6^{2}+8^{2}=36 + 64=100=10^{2}$,所以$\triangle PP'C$是直角三角形,且$\angle PP'C = 90^{\circ}$。
4. 最后,求$\angle APB$的度数:
由旋转性质可知$\angle APB=\angle CP'B$。
又因为$\angle CP'B=\angle BP'P+\angle PP'C$。
所以$\angle APB=60^{\circ}+90^{\circ}=150^{\circ}$。
故$\angle APB$的度数为$150^{\circ}$。
设旋转后$A$点与$C$点重合,$P$点旋转到$P'$点,连接$PP'$。
因为$\triangle ABC$是等边三角形,$\angle ABC = 60^{\circ}$,由旋转性质可知:$BP = BP'$,$\angle PBP'=60^{\circ}$,$AP = CP'=6$。
2. 然后,判断$\triangle BPP'$的形状:
在$\triangle BPP'$中,由于$BP = BP'$,$\angle PBP' = 60^{\circ}$,根据等边三角形的判定定理(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可得$\triangle BPP'$是等边三角形。
所以$PP'=BP = 8$,$\angle BP'P = 60^{\circ}$。
3. 接着,判断$\triangle PP'C$的形状:
在$\triangle PP'C$中,$PP' = 8$,$CP' = 6$,$PC = 10$。
根据勾股定理的逆定理$a^{2}+b^{2}=c^{2}$(其中$a = 6$,$b = 8$,$c = 10$),因为$6^{2}+8^{2}=36 + 64=100=10^{2}$,所以$\triangle PP'C$是直角三角形,且$\angle PP'C = 90^{\circ}$。
4. 最后,求$\angle APB$的度数:
由旋转性质可知$\angle APB=\angle CP'B$。
又因为$\angle CP'B=\angle BP'P+\angle PP'C$。
所以$\angle APB=60^{\circ}+90^{\circ}=150^{\circ}$。
故$\angle APB$的度数为$150^{\circ}$。
11. 如图3-25,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),且△A₁B₁C₁与△ABC关于原点O成中心对称.
(1) 画出△A₁B₁C₁,并写出A₁的坐标;
(2) P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对称点P'(a + 3,b + 1),请画出平移后的△A₂B₂C₂.

(1) 画出△A₁B₁C₁,并写出A₁的坐标;
(2) P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对称点P'(a + 3,b + 1),请画出平移后的△A₂B₂C₂.

答案:
【解析】:
(1) 关于原点对称的点的坐标特征是横、纵坐标都互为相反数。已知$A(-3,4)$,则$A_1(3,-4)$。根据$B(-4,2)$,$C(-2,1)$,可得$B_1(4,-2)$,$C_1(2,-1)$,然后连接$A_1B_1$,$B_1C_1$,$A_1C_1$,画出$\triangle A_1B_1C_1$。
(2) 点$P(a,b)$平移后得到$P'(a + 3,b + 1)$,说明$\triangle ABC$向右平移$3$个单位,向上平移$1$个单位。则$A(-3,4)$平移后$A_2(0,5)$,$B(-4,2)$平移后$B_2(-1,3)$,$C(-2,1)$平移后$C_2(1,2)$,连接$A_2B_2$,$B_2C_2$,$A_2C_2$,画出$\triangle A_2B_2C_2$。
【答案】:
(1) $A_1$的坐标为$(3,-4)$;
(2) 按上述平移方法画出$\triangle A_2B_2C_2$。
(1) 关于原点对称的点的坐标特征是横、纵坐标都互为相反数。已知$A(-3,4)$,则$A_1(3,-4)$。根据$B(-4,2)$,$C(-2,1)$,可得$B_1(4,-2)$,$C_1(2,-1)$,然后连接$A_1B_1$,$B_1C_1$,$A_1C_1$,画出$\triangle A_1B_1C_1$。
(2) 点$P(a,b)$平移后得到$P'(a + 3,b + 1)$,说明$\triangle ABC$向右平移$3$个单位,向上平移$1$个单位。则$A(-3,4)$平移后$A_2(0,5)$,$B(-4,2)$平移后$B_2(-1,3)$,$C(-2,1)$平移后$C_2(1,2)$,连接$A_2B_2$,$B_2C_2$,$A_2C_2$,画出$\triangle A_2B_2C_2$。
【答案】:
(1) $A_1$的坐标为$(3,-4)$;
(2) 按上述平移方法画出$\triangle A_2B_2C_2$。
查看更多完整答案,请扫码查看


