10. 将一个含45°角的三角板ABC如图3-36所示摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B'恰好落在x轴上,若点C的坐标为(1,0),则点B'的坐标为____.


答案:
$(3,0)$
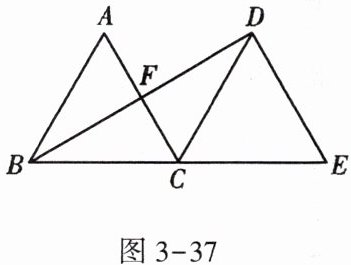
11. 如图3-37,△ABC是等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.猜想AC与BD的位置关系,并证明你的结论.

答案:
【解析】:
因为$\triangle ABC$是等边三角形,沿直线$BC$向右平移得到$\triangle DCE$,所以$AB = BC = CD = CE$,$\angle ABC=\angle DCE = 60^{\circ}$。
那么$\angle BCD = 180^{\circ}-\angle DCE=120^{\circ}$,又因为$BC = CD$,所以$\angle CBD=\angle CDB = 30^{\circ}$。
而$\angle ACB = 60^{\circ}$,在$\triangle BFC$中,$\angle BFC=180^{\circ}-\angle CBD - \angle ACB=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$。
【答案】:
$AC\perp BD$。
因为$\triangle ABC$是等边三角形,沿直线$BC$向右平移得到$\triangle DCE$,所以$AB = BC = CD = CE$,$\angle ABC=\angle DCE = 60^{\circ}$。
那么$\angle BCD = 180^{\circ}-\angle DCE=120^{\circ}$,又因为$BC = CD$,所以$\angle CBD=\angle CDB = 30^{\circ}$。
而$\angle ACB = 60^{\circ}$,在$\triangle BFC$中,$\angle BFC=180^{\circ}-\angle CBD - \angle ACB=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$。
【答案】:
$AC\perp BD$。
12. 如图3-38,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A₁OB₁.
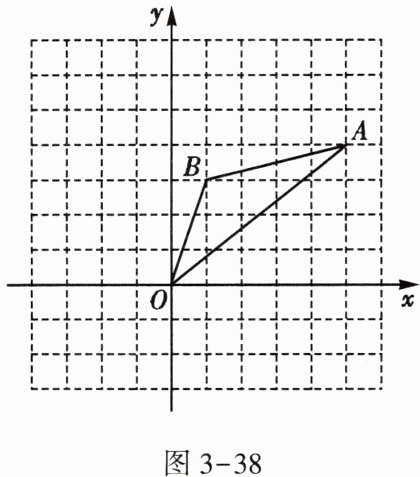
(1) 画出△A₁OB₁;
(2) 在旋转过程中点B所经过的路径长为____;
(3) 求在旋转过程中线段AB,BO扫过的图形的面积之和.

(1) 画出△A₁OB₁;
(2) 在旋转过程中点B所经过的路径长为____;
(3) 求在旋转过程中线段AB,BO扫过的图形的面积之和.
答案:
【解析】:
### $(1)$ 画出$\triangle A_{1}OB_{1}$
根据旋转的性质,点$(x,y)$绕原点$O$逆时针旋转$90^{\circ}$后得到的点坐标为$(-y,x)$。
已知$A(5,4)$,$B(1,3)$,则$A$绕点$O$逆时针旋转$90^{\circ}$后$A_{1}$的坐标为$( - 4,5)$,$B$绕点$O$逆时针旋转$90^{\circ}$后$B_{1}$的坐标为$( - 3,1)$。
连接$OA_{1}$,$OB_{1}$,$A_{1}B_{1}$,得到$\triangle A_{1}OB_{1}$。
### $(2)$ 求点$B$所经过的路径长
点$B$所经过的路径是以$O$为圆心,$OB$为半径的一段弧。
先求$OB$的长度,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,$O(0,0)$,$B(1,3)$,则$OB=\sqrt{1^{2}+3^{2}}=\sqrt{1 + 9}=\sqrt{10}$。
因为旋转角为$90^{\circ}$,根据弧长公式$l=\frac{n\pi r}{180}$($n$是圆心角,$r$是半径),这里$n = 90^{\circ}$,$r = OB=\sqrt{10}$,所以点$B$所经过的路径长$l=\frac{90\pi\times\sqrt{10}}{180}=\frac{\sqrt{10}\pi}{2}$。
### $(3)$ 求线段$AB$,$BO$扫过的图形的面积之和
线段$AB$,$BO$扫过的图形的面积之和等于扇形$AOA_{1}$的面积减去扇形$BOB_{1}$的面积。
由$A(5,4)$,根据两点间距离公式可得$OA=\sqrt{5^{2}+4^{2}}=\sqrt{25 + 16}=\sqrt{41}$,$OB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$。
根据扇形面积公式$S=\frac{n\pi r^{2}}{360}$($n$是圆心角,$r$是半径),这里$n = 90^{\circ}$。
扇形$AOA_{1}$的面积$S_{1}=\frac{90\pi\times(\sqrt{41})^{2}}{360}=\frac{41\pi}{4}$,扇形$BOB_{1}$的面积$S_{2}=\frac{90\pi\times(\sqrt{10})^{2}}{360}=\frac{10\pi}{4}$。
则线段$AB$,$BO$扫过的图形的面积之和$S = S_{1}-S_{2}=\frac{41\pi}{4}-\frac{10\pi}{4}=\frac{31\pi}{4}$。
【答案】:
$(1)$ 略(按上述坐标画出图形);
$(2)$ $\boldsymbol{\frac{\sqrt{10}\pi}{2}}$;
$(3)$ $\boldsymbol{\frac{31\pi}{4}}$。
### $(1)$ 画出$\triangle A_{1}OB_{1}$
根据旋转的性质,点$(x,y)$绕原点$O$逆时针旋转$90^{\circ}$后得到的点坐标为$(-y,x)$。
已知$A(5,4)$,$B(1,3)$,则$A$绕点$O$逆时针旋转$90^{\circ}$后$A_{1}$的坐标为$( - 4,5)$,$B$绕点$O$逆时针旋转$90^{\circ}$后$B_{1}$的坐标为$( - 3,1)$。
连接$OA_{1}$,$OB_{1}$,$A_{1}B_{1}$,得到$\triangle A_{1}OB_{1}$。
### $(2)$ 求点$B$所经过的路径长
点$B$所经过的路径是以$O$为圆心,$OB$为半径的一段弧。
先求$OB$的长度,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,$O(0,0)$,$B(1,3)$,则$OB=\sqrt{1^{2}+3^{2}}=\sqrt{1 + 9}=\sqrt{10}$。
因为旋转角为$90^{\circ}$,根据弧长公式$l=\frac{n\pi r}{180}$($n$是圆心角,$r$是半径),这里$n = 90^{\circ}$,$r = OB=\sqrt{10}$,所以点$B$所经过的路径长$l=\frac{90\pi\times\sqrt{10}}{180}=\frac{\sqrt{10}\pi}{2}$。
### $(3)$ 求线段$AB$,$BO$扫过的图形的面积之和
线段$AB$,$BO$扫过的图形的面积之和等于扇形$AOA_{1}$的面积减去扇形$BOB_{1}$的面积。
由$A(5,4)$,根据两点间距离公式可得$OA=\sqrt{5^{2}+4^{2}}=\sqrt{25 + 16}=\sqrt{41}$,$OB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$。
根据扇形面积公式$S=\frac{n\pi r^{2}}{360}$($n$是圆心角,$r$是半径),这里$n = 90^{\circ}$。
扇形$AOA_{1}$的面积$S_{1}=\frac{90\pi\times(\sqrt{41})^{2}}{360}=\frac{41\pi}{4}$,扇形$BOB_{1}$的面积$S_{2}=\frac{90\pi\times(\sqrt{10})^{2}}{360}=\frac{10\pi}{4}$。
则线段$AB$,$BO$扫过的图形的面积之和$S = S_{1}-S_{2}=\frac{41\pi}{4}-\frac{10\pi}{4}=\frac{31\pi}{4}$。
【答案】:
$(1)$ 略(按上述坐标画出图形);
$(2)$ $\boldsymbol{\frac{\sqrt{10}\pi}{2}}$;
$(3)$ $\boldsymbol{\frac{31\pi}{4}}$。
查看更多完整答案,请扫码查看


