5. 如图1 - 9,AB = AD,∠ABC = ∠ADC = 90°,EF过点C,BE⊥EF于点E,DF⊥EF于点F,BE = DF.求证:Rt△BCE≌Rt△DCF.


答案:
解:连接$BD$。
因为$AB = AD$,所以$\angle ABD=\angle ADB$。
又因为$\angle ABC=\angle ADC = 90^{\circ}$,所以$\angle ABC-\angle ABD=\angle ADC-\angle ADB$,即$\angle CBD=\angle CDB$,所以$BC = DC$。
在$Rt\triangle BCE$和$Rt\triangle DCF$中,$\left\{\begin{array}{l}BE = DF\\BC = DC\end{array}\right.$。
根据$HL$(斜边和一条直角边对应相等的两个直角三角形全等)定理,可得$Rt\triangle BCE\cong Rt\triangle DCF$。
因为$AB = AD$,所以$\angle ABD=\angle ADB$。
又因为$\angle ABC=\angle ADC = 90^{\circ}$,所以$\angle ABC-\angle ABD=\angle ADC-\angle ADB$,即$\angle CBD=\angle CDB$,所以$BC = DC$。
在$Rt\triangle BCE$和$Rt\triangle DCF$中,$\left\{\begin{array}{l}BE = DF\\BC = DC\end{array}\right.$。
根据$HL$(斜边和一条直角边对应相等的两个直角三角形全等)定理,可得$Rt\triangle BCE\cong Rt\triangle DCF$。
1. 如图1 - 10,AB//DF,AC⊥BC于点C,CB与DF交于点E,若∠A = 20°,则∠CEF等于( )

A. 110°
B. 100°
C. 80°
D. 70°

A. 110°
B. 100°
C. 80°
D. 70°
答案:
A
2. 将两张长方形纸片如图1 - 11所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1 + ∠2的度数为______.

答案:
$90^{\circ}$
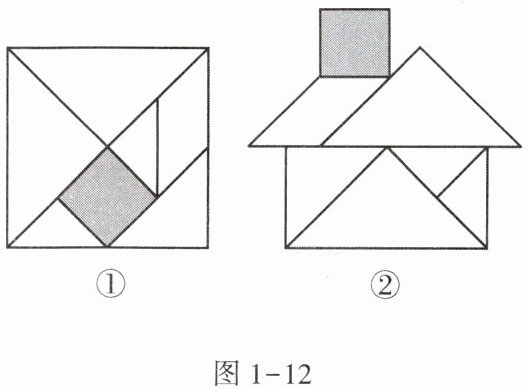
3. “七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”.图1 - 12①是由边长为10 cm的正方形薄板分为7块制作成的“七巧板”,图1 - 12②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为______(结果保留根号)cm.

答案:
【解析】:设正方形边长为$x cm$。
已知大正方形边长为$10 cm$,根据七巧板中图形的关系,大正方形的对角线长为$10\sqrt{2}cm$。
观察七巧板可知,小正方形的对角线长与两个小正方形边长之和存在关系,小正方形的对角线长为$\sqrt{2}x$,且$2x+\sqrt{2}x = 5\sqrt{2}$(大正方形对角线的一半是$5\sqrt{2}$)。
$(2 + \sqrt{2})x = 5\sqrt{2}$,
$x=\frac{5\sqrt{2}}{2 + \sqrt{2}}=\frac{5\sqrt{2}(2 - \sqrt{2})}{(2 + \sqrt{2})(2 - \sqrt{2})}=\frac{10\sqrt{2}-10}{4 - 2}=5\sqrt{2}-5$。
【答案】:$5\sqrt{2}-5$
已知大正方形边长为$10 cm$,根据七巧板中图形的关系,大正方形的对角线长为$10\sqrt{2}cm$。
观察七巧板可知,小正方形的对角线长与两个小正方形边长之和存在关系,小正方形的对角线长为$\sqrt{2}x$,且$2x+\sqrt{2}x = 5\sqrt{2}$(大正方形对角线的一半是$5\sqrt{2}$)。
$(2 + \sqrt{2})x = 5\sqrt{2}$,
$x=\frac{5\sqrt{2}}{2 + \sqrt{2}}=\frac{5\sqrt{2}(2 - \sqrt{2})}{(2 + \sqrt{2})(2 - \sqrt{2})}=\frac{10\sqrt{2}-10}{4 - 2}=5\sqrt{2}-5$。
【答案】:$5\sqrt{2}-5$
查看更多完整答案,请扫码查看


