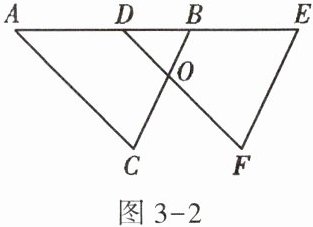
2. 如图3-2,平移△ABC可得到△DEF,如果∠A = 50°,∠C = 60°,那么∠E的度数为____,∠EDF的度数为____,∠F的度数为____,∠DOB的度数为____.

答案:
$70^{\circ}$,$50^{\circ}$,$60^{\circ}$,$60^{\circ}$
3. 小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数码经过平移其中一个能得到另一个,则这样的页共有____页.
答案:
$9$
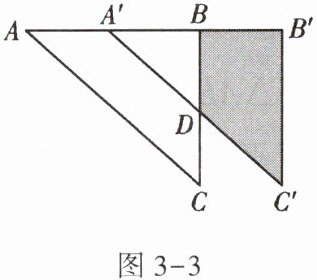
4. 如图3-3,△ABC经过平移得到△A'B'C',若四边形ACDA'的面积为6cm²,则阴影部分的面积为____.

答案:
$6cm^{2}$
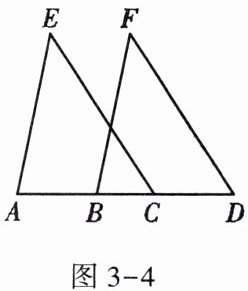
5. 如图3-4,点A,B,C,D在同一条直线上,AB = CD,∠D = ∠ECA,EC = FD.试说明AE = BF.

答案:
【解析】:
因为$AB = CD$,所以$AB + BC = CD + BC$,即$AC = BD$。
在$\triangle EAC$和$\triangle FBD$中,
$\begin{cases}EC = FD\\\angle ECA = \angle D\\AC = BD\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\triangle EAC\cong\triangle FBD$。
因为全等三角形的对应边相等,所以$AE = BF$。
【答案】:
$\because AB = CD$,$\therefore AB + BC = CD + BC$,即$AC = BD$。
在$\triangle EAC$和$\triangle FBD$中,$\begin{cases}EC = FD\\\angle ECA = \angle D\\AC = BD\end{cases}$,$\therefore\triangle EAC\cong\triangle FBD(SAS)$,$\therefore AE = BF$。
因为$AB = CD$,所以$AB + BC = CD + BC$,即$AC = BD$。
在$\triangle EAC$和$\triangle FBD$中,
$\begin{cases}EC = FD\\\angle ECA = \angle D\\AC = BD\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\triangle EAC\cong\triangle FBD$。
因为全等三角形的对应边相等,所以$AE = BF$。
【答案】:
$\because AB = CD$,$\therefore AB + BC = CD + BC$,即$AC = BD$。
在$\triangle EAC$和$\triangle FBD$中,$\begin{cases}EC = FD\\\angle ECA = \angle D\\AC = BD\end{cases}$,$\therefore\triangle EAC\cong\triangle FBD(SAS)$,$\therefore AE = BF$。
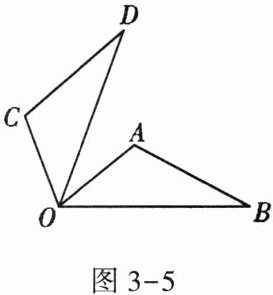
1. 如图3-5,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB = 40°,则∠AOD的度数为 ( )
A. 45°
B. 40°
C. 35°
D. 30°

A. 45°
B. 40°
C. 35°
D. 30°
答案:
D
查看更多完整答案,请扫码查看


