1. 若实数m,n满足等式|m - 2| + $\sqrt{n - 4}$ = 0,且m,n恰好是等腰三角形ABC的两条边的边长,则△ABC的周长是( )
A. 12
B. 10
C. 8
D. 6
A. 12
B. 10
C. 8
D. 6
答案:
1. 首先,根据绝对值与算术平方根的非负性:
因为$\vert m - 2\vert+\sqrt{n - 4}=0$,且$\vert m - 2\vert\geq0$,$\sqrt{n - 4}\geq0$。
所以当$\vert m - 2\vert = 0$且$\sqrt{n - 4}=0$时等式成立。
由$\vert m - 2\vert = 0$,可得$m−2 = 0$,解得$m = 2$;由$\sqrt{n - 4}=0$,可得$n−4 = 0$,解得$n = 4$。
2. 然后,根据等腰三角形的性质分情况讨论:
情况一:当$m = 2$为腰长时,三边长分别为$2$,$2$,$4$。
因为$2 + 2=4$,不满足三角形三边关系$a + b>c$(设$a = 2$,$b = 2$,$c = 4$),所以这种情况不能构成三角形。
情况二:当$n = 4$为腰长时,三边长分别为$2$,$4$,$4$。
此时$2+4>4$,$4 + 4>2$,满足三角形三边关系$a + b>c$($a = 2$,$b = 4$,$c = 4$)。
那么三角形$ABC$的周长$C=2 + 4+4$。
计算$C = 10$。
所以$\triangle ABC$的周长是$10$,答案是B。
因为$\vert m - 2\vert+\sqrt{n - 4}=0$,且$\vert m - 2\vert\geq0$,$\sqrt{n - 4}\geq0$。
所以当$\vert m - 2\vert = 0$且$\sqrt{n - 4}=0$时等式成立。
由$\vert m - 2\vert = 0$,可得$m−2 = 0$,解得$m = 2$;由$\sqrt{n - 4}=0$,可得$n−4 = 0$,解得$n = 4$。
2. 然后,根据等腰三角形的性质分情况讨论:
情况一:当$m = 2$为腰长时,三边长分别为$2$,$2$,$4$。
因为$2 + 2=4$,不满足三角形三边关系$a + b>c$(设$a = 2$,$b = 2$,$c = 4$),所以这种情况不能构成三角形。
情况二:当$n = 4$为腰长时,三边长分别为$2$,$4$,$4$。
此时$2+4>4$,$4 + 4>2$,满足三角形三边关系$a + b>c$($a = 2$,$b = 4$,$c = 4$)。
那么三角形$ABC$的周长$C=2 + 4+4$。
计算$C = 10$。
所以$\triangle ABC$的周长是$10$,答案是B。
2. 一个等腰三角形的一个外角等于110°,则这个三角形的顶角的度数为______.
答案:
1. 首先明确等腰三角形的性质:
等腰三角形两底角相等,三角形内角和为$180^{\circ}$,即$\angle A+\angle B + \angle C=180^{\circ}$(设$\angle A$为顶角,$\angle B=\angle C$为底角),且外角与它相邻的内角互补。
2. 然后分情况讨论:
情况一:若$110^{\circ}$的外角是顶角的外角**:
根据外角与内角互补,设顶角为$\alpha$,则$\alpha + 110^{\circ}=180^{\circ}$。
解得$\alpha=180^{\circ}-110^{\circ}=70^{\circ}$。
情况二:若$110^{\circ}$的外角是底角的外角**:
设底角为$\beta$,因为$\beta + 110^{\circ}=180^{\circ}$,所以$\beta = 180^{\circ}-110^{\circ}=70^{\circ}$。
又因为等腰三角形两底角相等,根据三角形内角和$\angle A+2\beta=180^{\circ}$($\angle A$为顶角),则顶角$\angle A=180^{\circ}-2\times70^{\circ}$。
计算$180^{\circ}-2\times70^{\circ}=180^{\circ}-140^{\circ}=40^{\circ}$。
所以这个三角形顶角的度数为$70^{\circ}$或$40^{\circ}$。
等腰三角形两底角相等,三角形内角和为$180^{\circ}$,即$\angle A+\angle B + \angle C=180^{\circ}$(设$\angle A$为顶角,$\angle B=\angle C$为底角),且外角与它相邻的内角互补。
2. 然后分情况讨论:
情况一:若$110^{\circ}$的外角是顶角的外角**:
根据外角与内角互补,设顶角为$\alpha$,则$\alpha + 110^{\circ}=180^{\circ}$。
解得$\alpha=180^{\circ}-110^{\circ}=70^{\circ}$。
情况二:若$110^{\circ}$的外角是底角的外角**:
设底角为$\beta$,因为$\beta + 110^{\circ}=180^{\circ}$,所以$\beta = 180^{\circ}-110^{\circ}=70^{\circ}$。
又因为等腰三角形两底角相等,根据三角形内角和$\angle A+2\beta=180^{\circ}$($\angle A$为顶角),则顶角$\angle A=180^{\circ}-2\times70^{\circ}$。
计算$180^{\circ}-2\times70^{\circ}=180^{\circ}-140^{\circ}=40^{\circ}$。
所以这个三角形顶角的度数为$70^{\circ}$或$40^{\circ}$。
3. 如图1 - 1,在△ABC中,AB = AD = DC,∠BAD = 20°,则∠C的度数为______.
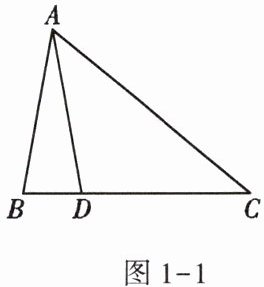

答案:
1. 首先,在$\triangle ABD$中:
已知$AB = AD$,根据等腰三角形的性质$\angle B=\angle ADB$。
由三角形内角和定理$\angle A+\angle B+\angle ADB = 180^{\circ}$,且$\angle BAD = 20^{\circ}$,设$\angle B=\angle ADB=x$,则$20^{\circ}+x + x=180^{\circ}$。
化简方程$2x=180^{\circ}-20^{\circ}=160^{\circ}$,解得$x = 80^{\circ}$,所以$\angle ADB = 80^{\circ}$。
2. 然后,求$\angle ADC$的度数:
因为$\angle ADB+\angle ADC = 180^{\circ}$(邻补角的定义),所以$\angle ADC=180^{\circ}-\angle ADB$。
把$\angle ADB = 80^{\circ}$代入,得$\angle ADC = 100^{\circ}$。
3. 最后,在$\triangle ADC$中:
已知$AD = DC$,根据等腰三角形的性质$\angle C=\angle DAC$。
再由三角形内角和定理$\angle ADC+\angle C+\angle DAC = 180^{\circ}$,设$\angle C = y$,则$\angle DAC = y$,所以$100^{\circ}+y + y=180^{\circ}$。
化简方程$2y=180^{\circ}-100^{\circ}=80^{\circ}$,解得$y = 40^{\circ}$。
所以$\angle C$的度数为$40^{\circ}$。
已知$AB = AD$,根据等腰三角形的性质$\angle B=\angle ADB$。
由三角形内角和定理$\angle A+\angle B+\angle ADB = 180^{\circ}$,且$\angle BAD = 20^{\circ}$,设$\angle B=\angle ADB=x$,则$20^{\circ}+x + x=180^{\circ}$。
化简方程$2x=180^{\circ}-20^{\circ}=160^{\circ}$,解得$x = 80^{\circ}$,所以$\angle ADB = 80^{\circ}$。
2. 然后,求$\angle ADC$的度数:
因为$\angle ADB+\angle ADC = 180^{\circ}$(邻补角的定义),所以$\angle ADC=180^{\circ}-\angle ADB$。
把$\angle ADB = 80^{\circ}$代入,得$\angle ADC = 100^{\circ}$。
3. 最后,在$\triangle ADC$中:
已知$AD = DC$,根据等腰三角形的性质$\angle C=\angle DAC$。
再由三角形内角和定理$\angle ADC+\angle C+\angle DAC = 180^{\circ}$,设$\angle C = y$,则$\angle DAC = y$,所以$100^{\circ}+y + y=180^{\circ}$。
化简方程$2y=180^{\circ}-100^{\circ}=80^{\circ}$,解得$y = 40^{\circ}$。
所以$\angle C$的度数为$40^{\circ}$。
4. 在△ABC中,若∠A = 80°,∠B = 50°,AC = 5,则AB的长度为______.
答案:
【解析】:在$\triangle ABC$中,已知$\angle A = 80^{\circ}$,$\angle B = 50^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle C=180^{\circ}-\angle A - \angle B=180^{\circ}-80^{\circ}-50^{\circ}=50^{\circ}$。
因为$\angle B = \angle C = 50^{\circ}$,所以$\triangle ABC$是等腰三角形,$AB = AC$。
又已知$AC = 5$,所以$AB = 5$。
【答案】:$5$
因为$\angle B = \angle C = 50^{\circ}$,所以$\triangle ABC$是等腰三角形,$AB = AC$。
又已知$AC = 5$,所以$AB = 5$。
【答案】:$5$
5. 如图1 - 2,在△ABC中,AB = BC,DE⊥AB于点E,FD⊥BC于点D,交AC于点F.
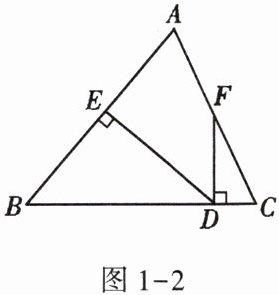
(1)若∠AFD = 155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD = $\frac{1}{2}$∠B.

(1)若∠AFD = 155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD = $\frac{1}{2}$∠B.
答案:
【解析】:
### $(1)$求$\angle EDF$的度数
- 首先求$\angle DFC$的度数:
已知$\angle AFD = 155^{\circ}$,因为$\angle AFD+\angle DFC = 180^{\circ}$(邻补角的定义),所以$\angle DFC=180^{\circ}-\angle AFD = 180^{\circ}- 155^{\circ}=25^{\circ}$。
- 然后求$\angle C$的度数:
因为$FD\perp BC$,在$Rt\triangle FDC$中,$\angle FDC = 90^{\circ}$,根据直角三角形两锐角互余,可得$\angle C=90^{\circ}-\angle DFC=90^{\circ}-25^{\circ} = 65^{\circ}$。
- 接着利用$AB = BC$求$\angle A$的度数:
因为$AB = BC$,所以$\angle A=\angle C = 65^{\circ}$(等边对等角)。
- 最后求$\angle EDF$的度数:
因为$DE\perp AB$,$FD\perp BC$,所以$\angle DEB=\angle FDC = 90^{\circ}$。
四边形$BEDF$内角和为$360^{\circ}$,$\angle B +\angle BED+\angle EDF+\angle BDF = 360^{\circ}$,又因为$\angle A+\angle B+\angle C = 180^{\circ}$,$\angle A=\angle C = 65^{\circ}$,所以$\angle B=180^{\circ}-(\angle A+\angle C)=180^{\circ}-(65^{\circ}+65^{\circ}) = 50^{\circ}$。
$\angle BED=\angle FDC = 90^{\circ}$,$\angle BDF = 90^{\circ}$,则$\angle EDF=360^{\circ}-\angle B - \angle BED-\angle BDF=360^{\circ}-50^{\circ}-90^{\circ}-90^{\circ}=130^{\circ}-90^{\circ}=50^{\circ}$。
### $(2)$证明$\angle CFD=\frac{1}{2}\angle B$
连接$BF$:
- 因为$AB = BC$,点$F$是$AC$的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的中线、底边上的高、顶角平分线互相重合),所以$BF\perp AC$,$\angle ABF=\angle CBF=\frac{1}{2}\angle ABC$。
- 又因为$\angle CFD+\angle BFD = 90^{\circ}$,$\angle CBF+\angle BFD = 90^{\circ}$(直角三角形两锐角互余)。
根据同角的余角相等,所以$\angle CFD=\angle CBF$,而$\angle CBF=\frac{1}{2}\angle ABC$,所以$\angle CFD=\frac{1}{2}\angle B$。
【答案】:
$(1)$$\boldsymbol{50^{\circ}}$;$(2)$证明过程如上述解析,证得$\angle CFD=\frac{1}{2}\angle B$。
### $(1)$求$\angle EDF$的度数
- 首先求$\angle DFC$的度数:
已知$\angle AFD = 155^{\circ}$,因为$\angle AFD+\angle DFC = 180^{\circ}$(邻补角的定义),所以$\angle DFC=180^{\circ}-\angle AFD = 180^{\circ}- 155^{\circ}=25^{\circ}$。
- 然后求$\angle C$的度数:
因为$FD\perp BC$,在$Rt\triangle FDC$中,$\angle FDC = 90^{\circ}$,根据直角三角形两锐角互余,可得$\angle C=90^{\circ}-\angle DFC=90^{\circ}-25^{\circ} = 65^{\circ}$。
- 接着利用$AB = BC$求$\angle A$的度数:
因为$AB = BC$,所以$\angle A=\angle C = 65^{\circ}$(等边对等角)。
- 最后求$\angle EDF$的度数:
因为$DE\perp AB$,$FD\perp BC$,所以$\angle DEB=\angle FDC = 90^{\circ}$。
四边形$BEDF$内角和为$360^{\circ}$,$\angle B +\angle BED+\angle EDF+\angle BDF = 360^{\circ}$,又因为$\angle A+\angle B+\angle C = 180^{\circ}$,$\angle A=\angle C = 65^{\circ}$,所以$\angle B=180^{\circ}-(\angle A+\angle C)=180^{\circ}-(65^{\circ}+65^{\circ}) = 50^{\circ}$。
$\angle BED=\angle FDC = 90^{\circ}$,$\angle BDF = 90^{\circ}$,则$\angle EDF=360^{\circ}-\angle B - \angle BED-\angle BDF=360^{\circ}-50^{\circ}-90^{\circ}-90^{\circ}=130^{\circ}-90^{\circ}=50^{\circ}$。
### $(2)$证明$\angle CFD=\frac{1}{2}\angle B$
连接$BF$:
- 因为$AB = BC$,点$F$是$AC$的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的中线、底边上的高、顶角平分线互相重合),所以$BF\perp AC$,$\angle ABF=\angle CBF=\frac{1}{2}\angle ABC$。
- 又因为$\angle CFD+\angle BFD = 90^{\circ}$,$\angle CBF+\angle BFD = 90^{\circ}$(直角三角形两锐角互余)。
根据同角的余角相等,所以$\angle CFD=\angle CBF$,而$\angle CBF=\frac{1}{2}\angle ABC$,所以$\angle CFD=\frac{1}{2}\angle B$。
【答案】:
$(1)$$\boldsymbol{50^{\circ}}$;$(2)$证明过程如上述解析,证得$\angle CFD=\frac{1}{2}\angle B$。
1. 如图1 - 3,在△ABC中,AB = AC,∠A = 36°,将△ABC中的∠A沿DE向下翻折,使点A落在点C处.若AE = $\sqrt{3}$,则BC的长是( )
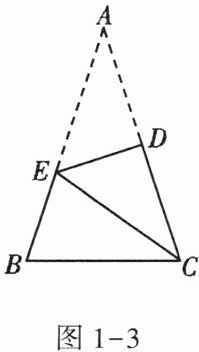
A. 1
B. 2
C. $\sqrt{3}$
D. 3

A. 1
B. 2
C. $\sqrt{3}$
D. 3
答案:
$\sqrt{3}$
查看更多完整答案,请扫码查看


