平行四边形
平行四边形的性质
边:对边______
角:对角______,邻角______
对角线:对角线______
对称性:平行四边形是______对称图形
平行四边形的判定
两组对边分别______的四边形是平行四边形
一组对边______的四边形是平行四边形
对角线______的四边形是平行四边形
三角形的中位线______第三边,且等于第三边的______
n边形的内角和为______,正n边形的每个内角为______
任何一个多边形的外角和都为______
平行四边形的性质
边:对边______
角:对角______,邻角______
对角线:对角线______
对称性:平行四边形是______对称图形
平行四边形的判定
两组对边分别______的四边形是平行四边形
一组对边______的四边形是平行四边形
对角线______的四边形是平行四边形
三角形的中位线______第三边,且等于第三边的______
n边形的内角和为______,正n边形的每个内角为______
任何一个多边形的外角和都为______
答案:
【解析】:本题主要考查平行四边形的性质、判定,三角形中位线定理以及多边形内角和与外角和的相关知识。
1. 平行四边形性质:
边的性质:根据平行四边形的定义和性质,平行四边形的对边平行且相等。
角的性质:平行四边形的对角相等,因为平行四边形的两组对边分别平行,利用平行线的性质可推出对角相等;邻角互补,因为两直线平行,同旁内角互补。
对角线性质:平行四边形的对角线互相平分,可通过全等三角形证明。
对称性:平行四边形是中心对称图形,绕着它的两条对角线的交点旋转$180^{\circ}$后能与原来的图形重合。
2. 平行四边形的判定:
两组对边分别平行的四边形是平行四边形,这是平行四边形的定义,也是最基本的判定方法。
一组对边平行且相等的四边形是平行四边形,可通过构造全等三角形等方法证明。
对角线互相平分的四边形是平行四边形,同样可通过全等三角形证明。
3. 三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半,可通过相似三角形或倍长中线等方法证明。
4. 多边形内角和与外角和:
$n$边形内角和公式为$(n - 2)\times180^{\circ}$,可通过从$n$边形的一个顶点出发,连接其余各顶点,将$n$边形分割成$(n - 2)$个三角形,利用三角形内角和为$180^{\circ}$推导得出。
正$n$边形的每个内角为$\frac{(n - 2)\times180^{\circ}}{n}$,因为正$n$边形的$n$个内角都相等,所以用内角和除以$n$即可得到每个内角的度数。
任何一个多边形的外角和都为$360^{\circ}$,与边数无关。
【答案】:平行且相等;相等;互补;互相平分;中心;平行;平行且相等;互相平分;平行于;一半;$(n - 2)\times180^{\circ}$;$\frac{(n - 2)\times180^{\circ}}{n}$;$360^{\circ}$
1. 平行四边形性质:
边的性质:根据平行四边形的定义和性质,平行四边形的对边平行且相等。
角的性质:平行四边形的对角相等,因为平行四边形的两组对边分别平行,利用平行线的性质可推出对角相等;邻角互补,因为两直线平行,同旁内角互补。
对角线性质:平行四边形的对角线互相平分,可通过全等三角形证明。
对称性:平行四边形是中心对称图形,绕着它的两条对角线的交点旋转$180^{\circ}$后能与原来的图形重合。
2. 平行四边形的判定:
两组对边分别平行的四边形是平行四边形,这是平行四边形的定义,也是最基本的判定方法。
一组对边平行且相等的四边形是平行四边形,可通过构造全等三角形等方法证明。
对角线互相平分的四边形是平行四边形,同样可通过全等三角形证明。
3. 三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半,可通过相似三角形或倍长中线等方法证明。
4. 多边形内角和与外角和:
$n$边形内角和公式为$(n - 2)\times180^{\circ}$,可通过从$n$边形的一个顶点出发,连接其余各顶点,将$n$边形分割成$(n - 2)$个三角形,利用三角形内角和为$180^{\circ}$推导得出。
正$n$边形的每个内角为$\frac{(n - 2)\times180^{\circ}}{n}$,因为正$n$边形的$n$个内角都相等,所以用内角和除以$n$即可得到每个内角的度数。
任何一个多边形的外角和都为$360^{\circ}$,与边数无关。
【答案】:平行且相等;相等;互补;互相平分;中心;平行;平行且相等;互相平分;平行于;一半;$(n - 2)\times180^{\circ}$;$\frac{(n - 2)\times180^{\circ}}{n}$;$360^{\circ}$
1. 如图6-1,在$\square ABCD$中,BF平分$\angle ABC$,交AD于点F,CE平分$\angle BCD$,交AD于点E,$AB = 6$,$EF = 2$,则BC长为()
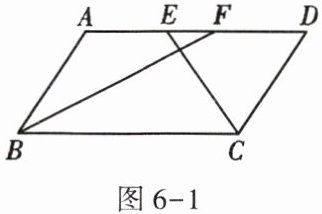
A. 8
B. 10
C. 12
D. 14

A. 8
B. 10
C. 12
D. 14
答案:
B
2. 如图6-2,在$\square ABCD$中,$\angle A = 70^{\circ}$,$DC = DB$,则$\angle CDB$的度数为()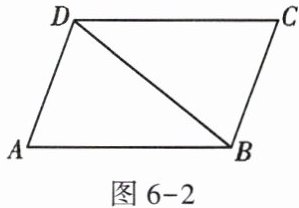
A. $40^{\circ}$
B. $50^{\circ}$
C. $60^{\circ}$
D. $70^{\circ}$

A. $40^{\circ}$
B. $50^{\circ}$
C. $60^{\circ}$
D. $70^{\circ}$
答案:
A
3. 如图6-3,将$\square ABCO$放置在平面直角坐标系$xOy$中,O为坐标原点,若点A的坐标是$(6,0)$,点C的坐标是$(1,4)$,则点B的坐标是______.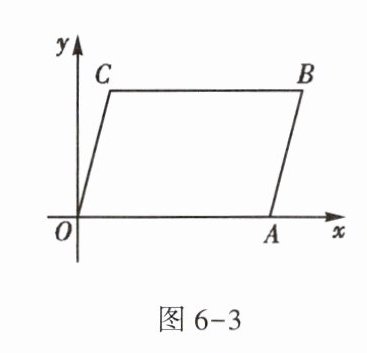

答案:
$(7,4)$
查看更多完整答案,请扫码查看


