《2025年暑假作业本大象出版社八年级数学北师大版》

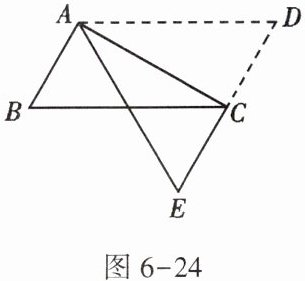
1. 如图6-24，在$\square ABCD$中，将$\triangle ADC$沿AC折叠后，点D恰好落在DC的延长线上的点E处.若$\angle B = 60^{\circ}$，$AB = 3$，则$\triangle ADE$的周长为()

A. 12
B. 15
C. 18
D. 21

答案： C

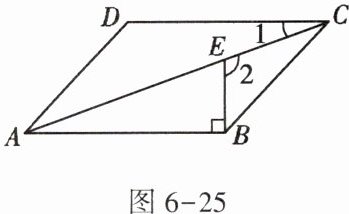
2. 如图6-25，在$\square ABCD$中，$BE \perp AB$交对角线AC于点E，若$\angle 1 = 20^{\circ}$，则$\angle 2$的度数为()

A. $110^{\circ}$
B. $120^{\circ}$
C. $135^{\circ}$
D. $140^{\circ}$

答案： A

3. 在$\square ABCD$中，$AB = 3$，$BC = 4$，当$\square ABCD$的面积最大时，有下列结论：①$AC = 5$；②$\angle A + \angle C = 180^{\circ}$；③$AC \perp BD$；④$AC = BD$.其中正确的有()
A. ①②③
B. ①②④
C. ②③④
D. ①③④

答案： B

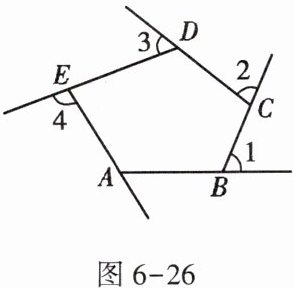
4. 如图6-26，$\angle 1$，$\angle 2$，$\angle 3$，$\angle 4$是五边形ABCDE的4个外角，若$\angle EAB = 120^{\circ}$，则$\angle 1 + \angle 2 + \angle 3 + \angle 4$等于()

A. $540^{\circ}$
B. $360^{\circ}$
C. $300^{\circ}$
D. $240^{\circ}$

答案： C

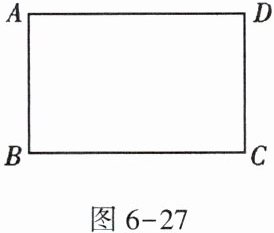
5. 图6-27为长方形ABCD，一条直线将该长方形分割成两个多边形，若这两个多边形的内角和分别为a和b，则$a + b$不可能是()

A. $360^{\circ}$
B. $540^{\circ}$
C. $630^{\circ}$
D. $720^{\circ}$

答案： C

6. 如图6-28，P是$\square ABCD$的边AD上一点，E，F分别是PB，PC的中点，若$\square ABCD$的面积为$16cm^{2}$，则$\triangle PEF$的面积(阴影部分)是______$cm^{2}$.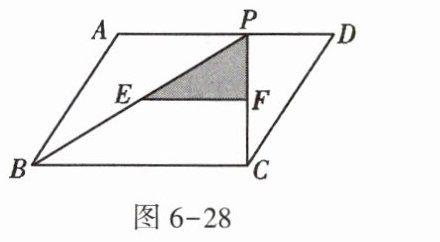

答案： $2$