《2025年暑假作业本大象出版社八年级数学北师大版》

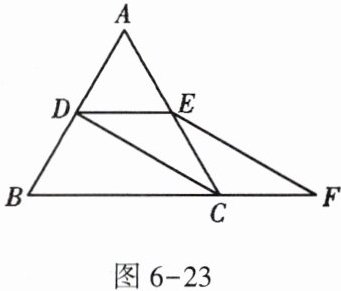
13. 如图6-23，等边三角形ABC的边长是2，D，E分别为AB，AC的中点，延长BC至点F，使$CF = \frac{1}{2}BC$，连接CD和EF.
(1)求证：四边形CDEF是平行四边形；
(2)求四边形BDEF的周长；
(3)求四边形CDEF的面积.

答案： 【解析】：
(1) 因为$D$、$E$分别为$AB$、$AC$的中点，所以$DE$是$\triangle ABC$的中位线。
根据三角形中位线定理：三角形的中位线平行于第三边且等于第三边的一半，可得$DE// BC$，$DE=\frac{1}{2}BC$。
又因为$CF = \frac{1}{2}BC$，所以$DE = CF$。
一组对边平行且相等的四边形是平行四边形，所以四边形$CDEF$是平行四边形。
(2) 已知等边三角形$ABC$边长$BC = 2$，$D$为$AB$中点，则$BD=\frac{1}{2}AB = 1$。
由
(1)知$DE=\frac{1}{2}BC = 1$，$CF=\frac{1}{2}BC = 1$，$EF = CD$。
因为$\triangle ABC$是等边三角形，$D$是$AB$中点，根据等边三角形三线合一性质，$CD\perp AB$，$AD = 1$，$AC = 2$。
根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$，所以$EF=\sqrt{3}$。
四边形$BDEF$的周长$=BD + DE+EF + BF=1 + 1+\sqrt{3}+(2 + 1)=5+\sqrt{3}$。
(3) $S_{\triangle ABC}=\frac{1}{2}\times AB\times CD=\frac{1}{2}\times2\times\sqrt{3}=\sqrt{3}$。
因为$DE$是$\triangle ABC$中位线，所以$S_{\triangle ADE}=\frac{1}{4}S_{\triangle ABC}=\frac{\sqrt{3}}{4}$。
$S_{\text{四边形}CDEF}=S_{\triangle ABC}-S_{\triangle ADE}=\sqrt{3}-\frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}$。
【答案】：
(1) 证明见上述解析；
(2) $5 + \sqrt{3}$；
(3) $\frac{3\sqrt{3}}{4}$。