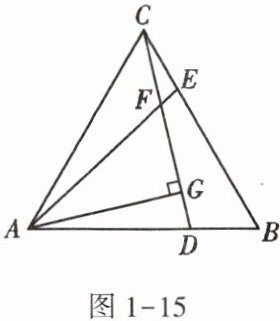
3. 如图1 - 15,在等边三角形ABC中,D,E分别为AB,BC边上的两动点,且总使AD = BE,AE与CD交于点F,AG⊥CD于点G,则$\frac{FG}{AF}$的值为______.

答案:
1. 首先证明$\triangle ABE\cong\triangle CAD$:
已知$\triangle ABC$是等边三角形,所以$AB = AC$,$\angle B=\angle CAD = 60^{\circ}$。
又因为$AD = BE$,根据$SAS$(边角边)判定定理,在$\triangle ABE$和$\triangle CAD$中,$\left\{\begin{array}{l}AB = AC\\\angle B=\angle CAD\\BE = AD\end{array}\right.$,则$\triangle ABE\cong\triangle CAD$。
由全等三角形的性质可得$\angle BAE=\angle ACD$。
2. 然后求$\angle AFG$的度数:
根据三角形外角性质,$\angle AFG=\angle FAC+\angle ACD$。
因为$\angle BAE=\angle ACD$,所以$\angle AFG=\angle FAC+\angle BAE$。
而$\angle FAC+\angle BAE=\angle BAC$,又因为$\angle BAC = 60^{\circ}$,所以$\angle AFG = 60^{\circ}$。
3. 最后在$Rt\triangle AFG$中求$\frac{FG}{AF}$的值:
在$Rt\triangle AFG$中,$\angle AGF = 90^{\circ}$,$\angle AFG = 60^{\circ}$,根据三角函数的定义$\cos\angle AFG=\frac{FG}{AF}$。
因为$\cos60^{\circ}=\frac{1}{2}$。
所以$\frac{FG}{AF}$的值为$\frac{1}{2}$。
已知$\triangle ABC$是等边三角形,所以$AB = AC$,$\angle B=\angle CAD = 60^{\circ}$。
又因为$AD = BE$,根据$SAS$(边角边)判定定理,在$\triangle ABE$和$\triangle CAD$中,$\left\{\begin{array}{l}AB = AC\\\angle B=\angle CAD\\BE = AD\end{array}\right.$,则$\triangle ABE\cong\triangle CAD$。
由全等三角形的性质可得$\angle BAE=\angle ACD$。
2. 然后求$\angle AFG$的度数:
根据三角形外角性质,$\angle AFG=\angle FAC+\angle ACD$。
因为$\angle BAE=\angle ACD$,所以$\angle AFG=\angle FAC+\angle BAE$。
而$\angle FAC+\angle BAE=\angle BAC$,又因为$\angle BAC = 60^{\circ}$,所以$\angle AFG = 60^{\circ}$。
3. 最后在$Rt\triangle AFG$中求$\frac{FG}{AF}$的值:
在$Rt\triangle AFG$中,$\angle AGF = 90^{\circ}$,$\angle AFG = 60^{\circ}$,根据三角函数的定义$\cos\angle AFG=\frac{FG}{AF}$。
因为$\cos60^{\circ}=\frac{1}{2}$。
所以$\frac{FG}{AF}$的值为$\frac{1}{2}$。
4. 在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若∠C = 90°,∠B = 30°,a - b = 2,则c = ______.
答案:
1. 首先,根据直角三角形的性质:
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,根据“在直角三角形中,如果一个锐角等于$30^{\circ}$,那么它所对的直角边等于斜边的一半”,可得$b=\frac{1}{2}c$。
再根据勾股定理$a^{2}+b^{2}=c^{2}$,则$a=\sqrt{c^{2}-b^{2}}$,把$b = \frac{1}{2}c$代入可得$a=\sqrt{c^{2}-\left(\frac{1}{2}c\right)^{2}}=\sqrt{\frac{4c^{2}-c^{2}}{4}}=\sqrt{\frac{3c^{2}}{4}}=\frac{\sqrt{3}}{2}c$。
2. 然后,利用已知条件$a - b = 2$:
把$a=\frac{\sqrt{3}}{2}c$,$b=\frac{1}{2}c$代入$a - b = 2$中,得到$\frac{\sqrt{3}}{2}c-\frac{1}{2}c = 2$。
提取公因式$c$,即$c\left(\frac{\sqrt{3}-1}{2}\right)=2$。
则$c=\frac{4}{\sqrt{3}-1}$。
对$\frac{4}{\sqrt{3}-1}$进行分母有理化,分子分母同时乘以$\sqrt{3}+1$,根据$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=\sqrt{3}$,$n = 1$,则$c=\frac{4(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$。
因为$(\sqrt{3}-1)(\sqrt{3}+1)=(\sqrt{3})^{2}-1^{2}=3 - 1 = 2$,所以$c = 2(\sqrt{3}+1)=2\sqrt{3}+2$。
故答案为$2\sqrt{3}+2$。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,根据“在直角三角形中,如果一个锐角等于$30^{\circ}$,那么它所对的直角边等于斜边的一半”,可得$b=\frac{1}{2}c$。
再根据勾股定理$a^{2}+b^{2}=c^{2}$,则$a=\sqrt{c^{2}-b^{2}}$,把$b = \frac{1}{2}c$代入可得$a=\sqrt{c^{2}-\left(\frac{1}{2}c\right)^{2}}=\sqrt{\frac{4c^{2}-c^{2}}{4}}=\sqrt{\frac{3c^{2}}{4}}=\frac{\sqrt{3}}{2}c$。
2. 然后,利用已知条件$a - b = 2$:
把$a=\frac{\sqrt{3}}{2}c$,$b=\frac{1}{2}c$代入$a - b = 2$中,得到$\frac{\sqrt{3}}{2}c-\frac{1}{2}c = 2$。
提取公因式$c$,即$c\left(\frac{\sqrt{3}-1}{2}\right)=2$。
则$c=\frac{4}{\sqrt{3}-1}$。
对$\frac{4}{\sqrt{3}-1}$进行分母有理化,分子分母同时乘以$\sqrt{3}+1$,根据$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=\sqrt{3}$,$n = 1$,则$c=\frac{4(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$。
因为$(\sqrt{3}-1)(\sqrt{3}+1)=(\sqrt{3})^{2}-1^{2}=3 - 1 = 2$,所以$c = 2(\sqrt{3}+1)=2\sqrt{3}+2$。
故答案为$2\sqrt{3}+2$。
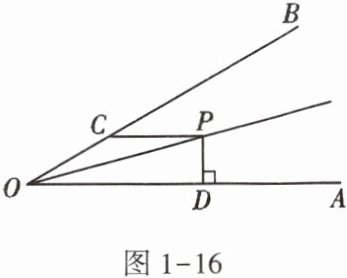
5. 如图1 - 16,∠AOB = 30°,OP是其角平分线,PC//OA,PD⊥OA,若PD = 1,求PC的长度.

答案:
【解析】:过点$P$作$PE\perp OB$于点$E$。
因为$OP$是$\angle AOB$的角平分线,$PD\perp OA$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PE = PD = 1$。
因为$PC// OA$,所以$\angle CPO=\angle POD$。
又因为$OP$平分$\angle AOB$,$\angle AOB = 30^{\circ}$,所以$\angle POD=\angle POC = 15^{\circ}$,则$\angle CPO=\angle POC = 15^{\circ}$。
所以$\angle BCP=\angle CPO+\angle POC=30^{\circ}$。
在$Rt\triangle PCE$中,$\angle BCP = 30^{\circ}$,根据在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半,可得$PC = 2PE$。
因为$PE = 1$,所以$PC = 2$。
【答案】:$2$
因为$OP$是$\angle AOB$的角平分线,$PD\perp OA$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PE = PD = 1$。
因为$PC// OA$,所以$\angle CPO=\angle POD$。
又因为$OP$平分$\angle AOB$,$\angle AOB = 30^{\circ}$,所以$\angle POD=\angle POC = 15^{\circ}$,则$\angle CPO=\angle POC = 15^{\circ}$。
所以$\angle BCP=\angle CPO+\angle POC=30^{\circ}$。
在$Rt\triangle PCE$中,$\angle BCP = 30^{\circ}$,根据在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半,可得$PC = 2PE$。
因为$PE = 1$,所以$PC = 2$。
【答案】:$2$
1. 如图1 - 17,在△ABC中,∠B = 40°,AC的垂直平分线交AC于点D,交BC于点E,且∠EAB : ∠CAE = 3 : 1,则∠C等于( )
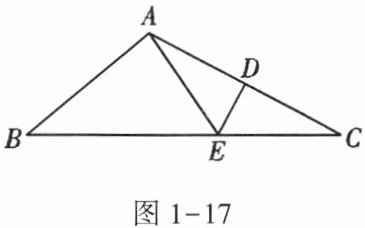
A. 28°
B. 25°
C. 22.5°
D. 20°

A. 28°
B. 25°
C. 22.5°
D. 20°
答案:
A
2. 已知△ABC(AC < BC),用尺规作图的方法在BC上确定一点P,使PA + PC = BC,则符合要求的作图痕迹是图1 - 18中的( )


答案:
B
3. 如图1 - 19,在△ABC中,AB + AC = 8 cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为______ cm.


答案:
1. 首先,根据线段垂直平分线的性质:
因为$l$是$BC$的垂直平分线,根据线段垂直平分线的性质定理$:$线段垂直平分线上的点到这条线段的两个端点的距离相等,所以$DB = DC$。
2. 然后,计算$\triangle ABD$的周长:
$\triangle ABD$的周长$C_{\triangle ABD}=AB + BD+AD$。
把$BD = DC$代入上式,可得$C_{\triangle ABD}=AB + DC + AD$。
又因为$DC + AD=AC$($A$、$D$、$C$三点共线),所以$C_{\triangle ABD}=AB + AC$。
3. 最后,已知条件代入:
已知$AB + AC = 8cm$。
所以$\triangle ABD$的周长为$8cm$。
因为$l$是$BC$的垂直平分线,根据线段垂直平分线的性质定理$:$线段垂直平分线上的点到这条线段的两个端点的距离相等,所以$DB = DC$。
2. 然后,计算$\triangle ABD$的周长:
$\triangle ABD$的周长$C_{\triangle ABD}=AB + BD+AD$。
把$BD = DC$代入上式,可得$C_{\triangle ABD}=AB + DC + AD$。
又因为$DC + AD=AC$($A$、$D$、$C$三点共线),所以$C_{\triangle ABD}=AB + AC$。
3. 最后,已知条件代入:
已知$AB + AC = 8cm$。
所以$\triangle ABD$的周长为$8cm$。
查看更多完整答案,请扫码查看


