13. 操作发现
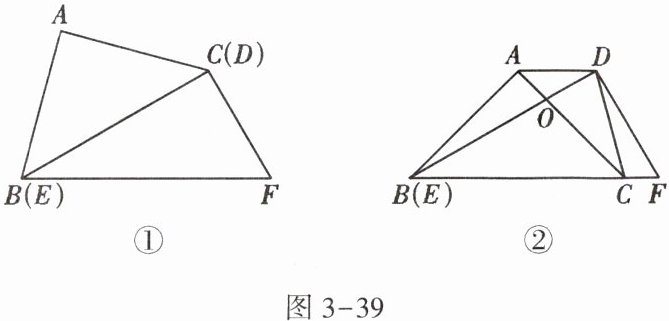
将一副直角三角板如图3-39①摆放,能够发现等腰直角三角板ABC的斜边BC与30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图3-39①中的等腰三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图3-39②.
(1) 求证:△CDO是等腰三角形;
(2) 若DF = 2√3,求AC的长.
将一副直角三角板如图3-39①摆放,能够发现等腰直角三角板ABC的斜边BC与30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图3-39①中的等腰三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图3-39②.
(1) 求证:△CDO是等腰三角形;
(2) 若DF = 2√3,求AC的长.

答案:
【解析】:
(1) 由题意可知$BC = DE$,$\angle DEF = 30^{\circ}$,所以$\angle BDC=\angle BCD = 75^{\circ}$。
因为$\angle ACB = 45^{\circ}$,所以$\angle DOC = 30^{\circ}+45^{\circ}=75^{\circ}$。
所以$\angle DOC=\angle BDC$,所以$\triangle CDO$是等腰三角形。
(2) 因为$\angle DEF = 30^{\circ}$,$DF = 2\sqrt{3}$,所以$DE = 6$,即$BC = 6$。
因为$\triangle ABC$是等腰直角三角形,所以$AC = BC\cdot\sin45^{\circ}=6\times\frac{\sqrt{2}}{2}=3\sqrt{2}$。
【答案】:
(1) 证明见上述解析。
(2) $3\sqrt{2}$
(1) 由题意可知$BC = DE$,$\angle DEF = 30^{\circ}$,所以$\angle BDC=\angle BCD = 75^{\circ}$。
因为$\angle ACB = 45^{\circ}$,所以$\angle DOC = 30^{\circ}+45^{\circ}=75^{\circ}$。
所以$\angle DOC=\angle BDC$,所以$\triangle CDO$是等腰三角形。
(2) 因为$\angle DEF = 30^{\circ}$,$DF = 2\sqrt{3}$,所以$DE = 6$,即$BC = 6$。
因为$\triangle ABC$是等腰直角三角形,所以$AC = BC\cdot\sin45^{\circ}=6\times\frac{\sqrt{2}}{2}=3\sqrt{2}$。
【答案】:
(1) 证明见上述解析。
(2) $3\sqrt{2}$
查看更多完整答案,请扫码查看


