6. 若E,F分别为任意四边形ABCD的边AD,BC的中点,则EF______(填“$\geqslant$”“$\leqslant$”或“$=$”)$\frac{1}{2}(AB + CD)$.
答案:
$\leqslant$
7. 如图6-18,在$\square ABCD$中,$\angle ADO = 90^{\circ}$,$OA = 6cm$,$OB = 3cm$,那么$AD =$______cm,$AC =$______cm.


答案:
$3\sqrt{3}$,$12$
8. 如图6-19,在$\triangle ABC$中,点D,E分别是AB,AC的中点,$\angle A = 50^{\circ}$,$\angle ADE = 60^{\circ}$,则$\angle C$的度数为______.


答案:
$70^{\circ}$
9. 若一个多边形的内角和是外角和的5倍,则这个多边形是______边形.
答案:
十二
10. 如图6-20,在四边形ABCD中,$AB = CD$,再添加一个条件______(写出一个即可),则四边形ABCD是平行四边形.(图形中不再添加辅助线)


答案:
$AB// CD$(或$AD = BC$等)
11. 如图6-21,点E是$\square ABCD$的边CD的中点,AE,BC的延长线交于点F,$CF = 3$,$CE = 2$,求$\square ABCD$的周长.

答案:
【解析】:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,$AB = CD$,$AD = BC$。
由于$AD// BC$,那么$\angle DAE=\angle F$,$\angle D=\angle ECF$。
又因为点$E$是$CD$的中点,所以$DE = CE = 2$,则$CD=DE + CE=4$。
在$\triangle ADE$和$\triangle FCE$中:
$\begin{cases}\angle DAE=\angle F\\\angle D=\angle ECF\\DE = CE\end{cases}$
所以$\triangle ADE\cong\triangle FCE(AAS)$。
根据全等三角形的性质,可得$AD = CF = 3$。
因为$AD = BC = 3$,$AB = CD = 4$,所以平行四边形$ABCD$的周长为$2(AB + BC)=2\times(4 + 3)=14$。
【答案】:$14$
因为四边形$ABCD$是平行四边形,所以$AD// BC$,$AB = CD$,$AD = BC$。
由于$AD// BC$,那么$\angle DAE=\angle F$,$\angle D=\angle ECF$。
又因为点$E$是$CD$的中点,所以$DE = CE = 2$,则$CD=DE + CE=4$。
在$\triangle ADE$和$\triangle FCE$中:
$\begin{cases}\angle DAE=\angle F\\\angle D=\angle ECF\\DE = CE\end{cases}$
所以$\triangle ADE\cong\triangle FCE(AAS)$。
根据全等三角形的性质,可得$AD = CF = 3$。
因为$AD = BC = 3$,$AB = CD = 4$,所以平行四边形$ABCD$的周长为$2(AB + BC)=2\times(4 + 3)=14$。
【答案】:$14$
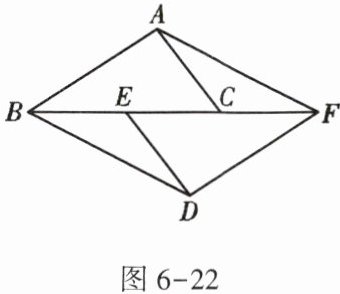
12. 如图6-22,点B,E,C,F在一条直线上,$AB = DF$,$AC = DE$,$BE = FC$.
(1)求证:$\triangle ABC \cong \triangle DFE$;
(2)连接AF,BD,求证:四边形ABDF是平行四边形.
(1)求证:$\triangle ABC \cong \triangle DFE$;
(2)连接AF,BD,求证:四边形ABDF是平行四边形.

答案:
【解析】:
### $(1)$ 证明$\triangle ABC\cong\triangle DFE$
已知$BE = FC$,根据等式的性质,在等式两边同时加上$EC$,可得$BE + EC=FC + EC$,即$BC = FE$。
在$\triangle ABC$和$\triangle DFE$中:
$\begin{cases}AB = DF\\AC = DE\\BC = FE\end{cases}$
根据“边 - 边 - 边”($SSS$)全等判定定理,所以$\triangle ABC\cong\triangle DFE$。
### $(2)$ 证明四边形$ABDF$是平行四边形
由$(1)$已证$\triangle ABC\cong\triangle DFE$,根据全等三角形的性质,全等三角形的对应角相等,所以$\angle ABC=\angle DFE$。
因为$\angle ABC$与$\angle DFE$是直线$AB$、$DF$被直线$BF$所截形成的同位角,同位角相等,两直线平行,所以$AB// DF$。
又因为已知$AB = DF$,根据“一组对边平行且相等的四边形是平行四边形”,所以四边形$ABDF$是平行四边形。
【答案】:
$(1)$ 证明见上述解析;$(2)$ 证明见上述解析。
### $(1)$ 证明$\triangle ABC\cong\triangle DFE$
已知$BE = FC$,根据等式的性质,在等式两边同时加上$EC$,可得$BE + EC=FC + EC$,即$BC = FE$。
在$\triangle ABC$和$\triangle DFE$中:
$\begin{cases}AB = DF\\AC = DE\\BC = FE\end{cases}$
根据“边 - 边 - 边”($SSS$)全等判定定理,所以$\triangle ABC\cong\triangle DFE$。
### $(2)$ 证明四边形$ABDF$是平行四边形
由$(1)$已证$\triangle ABC\cong\triangle DFE$,根据全等三角形的性质,全等三角形的对应角相等,所以$\angle ABC=\angle DFE$。
因为$\angle ABC$与$\angle DFE$是直线$AB$、$DF$被直线$BF$所截形成的同位角,同位角相等,两直线平行,所以$AB// DF$。
又因为已知$AB = DF$,根据“一组对边平行且相等的四边形是平行四边形”,所以四边形$ABDF$是平行四边形。
【答案】:
$(1)$ 证明见上述解析;$(2)$ 证明见上述解析。
查看更多完整答案,请扫码查看


