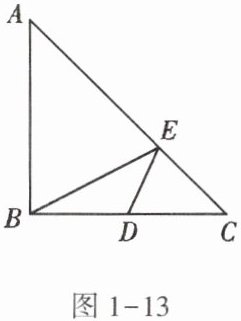
4. 如图1 - 13,在Rt△ABC中,AB = BC = 4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为______.

答案:
【解析】:
作点$B$关于$AC$的对称点$B'$,连接$B'D$交$AC$于点$E$,此时$\triangle BDE$的周长最小。
因为$AB = BC$,$\angle ABC = 90^{\circ}$,所以$\angle BCA = 45^{\circ}$。
由于点$B$与$B'$关于$AC$对称,所以$BC = B'C = 4$,$BE = B'E$,$\angle B'CA=\angle BCA = 45^{\circ}$,则$\angle BCB' = 90^{\circ}$。
已知$D$为$BC$中点,$BC = 4$,所以$BD = CD = 2$。
在$Rt\triangle B'CD$中,根据勾股定理$B'D=\sqrt{B'C^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$。
$\triangle BDE$的周长$=BD + DE + BE=BD + DE + B'E=BD + B'D$,$BD = 2$,所以$\triangle BDE$周长的最小值为$2 + 2\sqrt{5}$。
【答案】:$2 + 2\sqrt{5}$
作点$B$关于$AC$的对称点$B'$,连接$B'D$交$AC$于点$E$,此时$\triangle BDE$的周长最小。
因为$AB = BC$,$\angle ABC = 90^{\circ}$,所以$\angle BCA = 45^{\circ}$。
由于点$B$与$B'$关于$AC$对称,所以$BC = B'C = 4$,$BE = B'E$,$\angle B'CA=\angle BCA = 45^{\circ}$,则$\angle BCB' = 90^{\circ}$。
已知$D$为$BC$中点,$BC = 4$,所以$BD = CD = 2$。
在$Rt\triangle B'CD$中,根据勾股定理$B'D=\sqrt{B'C^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$。
$\triangle BDE$的周长$=BD + DE + BE=BD + DE + B'E=BD + B'D$,$BD = 2$,所以$\triangle BDE$周长的最小值为$2 + 2\sqrt{5}$。
【答案】:$2 + 2\sqrt{5}$
5. 如图1 - 14,在平面直角坐标系中,△AOB是直角三角形,∠AOB = 90°,斜边AB与y轴交于点C.
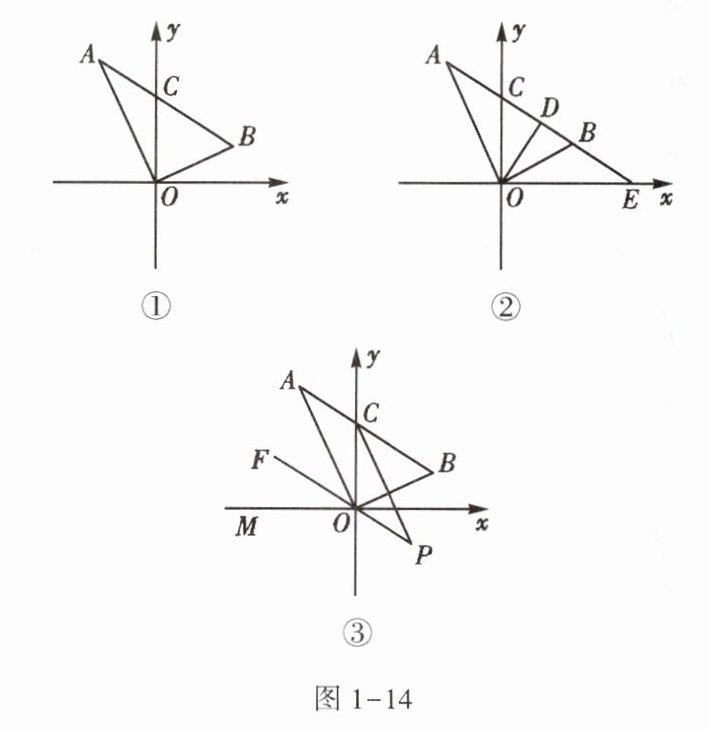
(1)若图1 - 14①中∠A = ∠AOC,求证:∠B = ∠BOC.
(2)图1 - 14②中延长AB交x轴于点E,过O作OD⊥AB,且∠DOB = ∠EOB,∠OAE = ∠OEA,求∠A的度数.
(3)如图1 - 14③,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),在(2)的条件下,∠P的度数是否发生改变?若不变,请求其度数;若改变,请说明理由.

(1)若图1 - 14①中∠A = ∠AOC,求证:∠B = ∠BOC.
(2)图1 - 14②中延长AB交x轴于点E,过O作OD⊥AB,且∠DOB = ∠EOB,∠OAE = ∠OEA,求∠A的度数.
(3)如图1 - 14③,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),在(2)的条件下,∠P的度数是否发生改变?若不变,请求其度数;若改变,请说明理由.
答案:
【解析】:
### $(1)$ 证明$\angle B = \angle BOC$
已知$\triangle AOB$是直角三角形,$\angle AOB = 90^{\circ}$,根据直角三角形两锐角互余,可得$\angle A+\angle B = 90^{\circ}$,$\angle AOC+\angle BOC = 90^{\circ}$。
又因为$\angle A=\angle AOC$,根据等角的余角相等,所以$\angle B=\angle BOC$。
### $(2)$ 求$\angle A$的度数
设$\angle A=\alpha$,因为$\angle OAE = \angle OEA$,所以$\angle EOA=\angle AOB - \angle EOB=90^{\circ}-\angle EOB$,且$\angle EOA = 180^{\circ}- 2\angle OEA=180^{\circ}-2\angle A = 180^{\circ}-2\alpha$。
因为$OD\perp AB$,所以$\angle DOB+\angle B = 90^{\circ}$,又$\angle A+\angle B = 90^{\circ}$,则$\angle DOB=\angle A$。
已知$\angle DOB=\angle EOB$,所以$\angle EOB=\angle A=\alpha$。
根据$\angle EOA+\angle EOB = 90^{\circ}$,即$(180^{\circ}-2\alpha)+\alpha = 90^{\circ}$。
化简方程$180^{\circ}-2\alpha+\alpha = 90^{\circ}$,可得$180^{\circ}-\alpha = 90^{\circ}$,解得$\alpha = 30^{\circ}$,所以$\angle A = 30^{\circ}$。
### $(3)$ 判断$\angle P$的度数是否改变并求解
因为$\angle A = 30^{\circ}$,所以$\angle AOM = 180^{\circ}-\angle AOC=180^{\circ}-(90^{\circ}-\angle A)= 90^{\circ}+\angle A = 120^{\circ}$。
由于$OF$平分$\angle AOM$,则$\angle FOM=\frac{1}{2}\angle AOM = 60^{\circ}$。
设$\angle ACO=\beta$,因为$CP$平分$\angle BCO$,$\angle BCO = 180^{\circ}-\beta$,所以$\angle PCO=\frac{1}{2}(180^{\circ}-\beta)=90^{\circ}-\frac{1}{2}\beta$。
又$\angle ACO=\angle A + \angle AOC$,$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC=90^{\circ}-\angle A$),所以$\beta=\angle A + 60^{\circ}=30^{\circ}+60^{\circ}=90^{\circ}$(这里$\beta$的推导也可根据三角形外角性质等)。
根据三角形外角性质,$\angle P=\angle PCO-\angle POM$,$\angle POM = \angle FOM = 60^{\circ}$,$\angle PCO=90^{\circ}-\frac{1}{2}\angle ACO$,$\angle ACO=\angle A + 60^{\circ}$($\angle A = 30^{\circ}$),$\angle ACO = 90^{\circ}$,$\angle PCO=45^{\circ}$,$\angle POM = 60^{\circ}$($\angle POM$与$\angle FOM$对顶角相等) 。
$\angle P=\angle PCO - \angle POM$,$\angle PCO = \frac{1}{2}(180^{\circ}-\angle ACO)$,$\angle ACO=\angle A+\angle AOC$,$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC = 90^{\circ}-\angle A$),$\angle ACO=90^{\circ}$,$\angle PCO = 45^{\circ}$,$\angle POM = 60^{\circ}$($\angle POM$与$\angle FOM$对顶角相等)。
$\angle P=\angle PCO-\angle POM$,由$\angle ACO=\angle A + \angle AOC$($\angle AOC = 90^{\circ}-\angle A$),$\angle PCO=\frac{1}{2}(180^{\circ}-\angle ACO)$,$\angle POM=\angle FOM$(对顶角相等),$\angle FOM=\frac{1}{2}\angle AOM$,$\angle AOM = 180^{\circ}-\angle AOC$。
$\angle P=\frac{1}{2}(180^{\circ}-\angle ACO)-\frac{1}{2}\angle AOM$,$\angle ACO=\angle A + \angle AOC$,$\angle AOM = 180^{\circ}-\angle AOC$,$\angle A = 30^{\circ}$,$\angle AOC = 60^{\circ}$。
$\angle P=\frac{1}{2}(180^{\circ}-(\angle A + 60^{\circ}))-\frac{1}{2}(180^{\circ}-60^{\circ})$
$=\frac{1}{2}(120^{\circ}-\angle A)-60^{\circ}$,把$\angle A = 30^{\circ}$代入得:
$\angle P=\frac{1}{2}(120^{\circ}-30^{\circ})-60^{\circ}=15^{\circ}$。
或者:
$\angle P = \angle PCO-\angle POC$,$\angle POC=\angle FOM = 60^{\circ}$(对顶角相等),$\angle PCO=\frac{1}{2}\angle BCO$,$\angle BCO=\angle A + \angle AOC$(外角性质),$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC=90^{\circ}-\angle A$),$\angle BCO = 90^{\circ}$,$\angle PCO = 45^{\circ}$,$\angle P=45^{\circ}- 30^{\circ}=15^{\circ}$。
【答案】:
$(1)$ 证明过程如上述;$(2)$$\boldsymbol{30^{\circ}}$;$(3)$ 不变,$\boldsymbol{15^{\circ}}$
### $(1)$ 证明$\angle B = \angle BOC$
已知$\triangle AOB$是直角三角形,$\angle AOB = 90^{\circ}$,根据直角三角形两锐角互余,可得$\angle A+\angle B = 90^{\circ}$,$\angle AOC+\angle BOC = 90^{\circ}$。
又因为$\angle A=\angle AOC$,根据等角的余角相等,所以$\angle B=\angle BOC$。
### $(2)$ 求$\angle A$的度数
设$\angle A=\alpha$,因为$\angle OAE = \angle OEA$,所以$\angle EOA=\angle AOB - \angle EOB=90^{\circ}-\angle EOB$,且$\angle EOA = 180^{\circ}- 2\angle OEA=180^{\circ}-2\angle A = 180^{\circ}-2\alpha$。
因为$OD\perp AB$,所以$\angle DOB+\angle B = 90^{\circ}$,又$\angle A+\angle B = 90^{\circ}$,则$\angle DOB=\angle A$。
已知$\angle DOB=\angle EOB$,所以$\angle EOB=\angle A=\alpha$。
根据$\angle EOA+\angle EOB = 90^{\circ}$,即$(180^{\circ}-2\alpha)+\alpha = 90^{\circ}$。
化简方程$180^{\circ}-2\alpha+\alpha = 90^{\circ}$,可得$180^{\circ}-\alpha = 90^{\circ}$,解得$\alpha = 30^{\circ}$,所以$\angle A = 30^{\circ}$。
### $(3)$ 判断$\angle P$的度数是否改变并求解
因为$\angle A = 30^{\circ}$,所以$\angle AOM = 180^{\circ}-\angle AOC=180^{\circ}-(90^{\circ}-\angle A)= 90^{\circ}+\angle A = 120^{\circ}$。
由于$OF$平分$\angle AOM$,则$\angle FOM=\frac{1}{2}\angle AOM = 60^{\circ}$。
设$\angle ACO=\beta$,因为$CP$平分$\angle BCO$,$\angle BCO = 180^{\circ}-\beta$,所以$\angle PCO=\frac{1}{2}(180^{\circ}-\beta)=90^{\circ}-\frac{1}{2}\beta$。
又$\angle ACO=\angle A + \angle AOC$,$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC=90^{\circ}-\angle A$),所以$\beta=\angle A + 60^{\circ}=30^{\circ}+60^{\circ}=90^{\circ}$(这里$\beta$的推导也可根据三角形外角性质等)。
根据三角形外角性质,$\angle P=\angle PCO-\angle POM$,$\angle POM = \angle FOM = 60^{\circ}$,$\angle PCO=90^{\circ}-\frac{1}{2}\angle ACO$,$\angle ACO=\angle A + 60^{\circ}$($\angle A = 30^{\circ}$),$\angle ACO = 90^{\circ}$,$\angle PCO=45^{\circ}$,$\angle POM = 60^{\circ}$($\angle POM$与$\angle FOM$对顶角相等) 。
$\angle P=\angle PCO - \angle POM$,$\angle PCO = \frac{1}{2}(180^{\circ}-\angle ACO)$,$\angle ACO=\angle A+\angle AOC$,$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC = 90^{\circ}-\angle A$),$\angle ACO=90^{\circ}$,$\angle PCO = 45^{\circ}$,$\angle POM = 60^{\circ}$($\angle POM$与$\angle FOM$对顶角相等)。
$\angle P=\angle PCO-\angle POM$,由$\angle ACO=\angle A + \angle AOC$($\angle AOC = 90^{\circ}-\angle A$),$\angle PCO=\frac{1}{2}(180^{\circ}-\angle ACO)$,$\angle POM=\angle FOM$(对顶角相等),$\angle FOM=\frac{1}{2}\angle AOM$,$\angle AOM = 180^{\circ}-\angle AOC$。
$\angle P=\frac{1}{2}(180^{\circ}-\angle ACO)-\frac{1}{2}\angle AOM$,$\angle ACO=\angle A + \angle AOC$,$\angle AOM = 180^{\circ}-\angle AOC$,$\angle A = 30^{\circ}$,$\angle AOC = 60^{\circ}$。
$\angle P=\frac{1}{2}(180^{\circ}-(\angle A + 60^{\circ}))-\frac{1}{2}(180^{\circ}-60^{\circ})$
$=\frac{1}{2}(120^{\circ}-\angle A)-60^{\circ}$,把$\angle A = 30^{\circ}$代入得:
$\angle P=\frac{1}{2}(120^{\circ}-30^{\circ})-60^{\circ}=15^{\circ}$。
或者:
$\angle P = \angle PCO-\angle POC$,$\angle POC=\angle FOM = 60^{\circ}$(对顶角相等),$\angle PCO=\frac{1}{2}\angle BCO$,$\angle BCO=\angle A + \angle AOC$(外角性质),$\angle AOC = 60^{\circ}$($\angle A = 30^{\circ}$,$\angle AOC=90^{\circ}-\angle A$),$\angle BCO = 90^{\circ}$,$\angle PCO = 45^{\circ}$,$\angle P=45^{\circ}- 30^{\circ}=15^{\circ}$。
【答案】:
$(1)$ 证明过程如上述;$(2)$$\boldsymbol{30^{\circ}}$;$(3)$ 不变,$\boldsymbol{15^{\circ}}$
1. 在△ABC中,∠B = 45°,∠A = 105°,AC = 6,则AB的长是( )
A. $3\sqrt{6}$
B. $3\sqrt{2}$
C. $2\sqrt{2}$
D. $6\sqrt{2}$
A. $3\sqrt{6}$
B. $3\sqrt{2}$
C. $2\sqrt{2}$
D. $6\sqrt{2}$
答案:
B
2. 已知等腰三角形的底角是30°,腰长为$2\sqrt{3}$,则它的周长是______.
答案:
【解析】:过等腰三角形的顶点作底边的垂线,根据等腰三角形三线合一的性质,这条垂线也是底边的中线。
在直角三角形中,已知腰长为$2\sqrt{3}$,底角是$30^{\circ}$,根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得底边的一半为$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=\sqrt{12 - 3}=\sqrt{9}=3$,那么底边的长为$2\times3 = 6$。
所以该等腰三角形的周长为$2\sqrt{3}+2\sqrt{3}+6 = 4\sqrt{3}+6$。
【答案】:$4\sqrt{3}+6$
在直角三角形中,已知腰长为$2\sqrt{3}$,底角是$30^{\circ}$,根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得底边的一半为$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=\sqrt{12 - 3}=\sqrt{9}=3$,那么底边的长为$2\times3 = 6$。
所以该等腰三角形的周长为$2\sqrt{3}+2\sqrt{3}+6 = 4\sqrt{3}+6$。
【答案】:$4\sqrt{3}+6$
查看更多完整答案,请扫码查看


