4. 如图1 - 27,△ABC是等腰三角形,AB = AC,∠BAC = 45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD',且点D',D,B三点在同一直线上,则∠ABD的度数是( )

A. 22.5°
B. 45°
C. 50°
D. 75°

A. 22.5°
B. 45°
C. 50°
D. 75°
答案:
A
5. 如图1 - 28,A,B是4×5网格中的格点,网格中的每个小正方形的边长都是1,图中使以A,B,C为顶点的三角形是等腰三角形的格点C有( )

A. 2个
B. 3个
C. 4个
D. 5个

A. 2个
B. 3个
C. 4个
D. 5个
答案:
D
6. 如图1 - 29,在△ABC中,AB = AC,BD和CD分别是∠ABC和∠ACB的平分线,EF过D点,且EF//BC,图中共有______个等腰三角形.
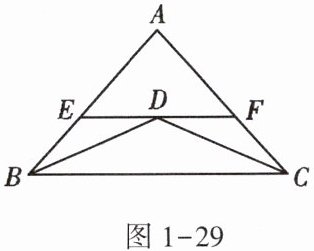

答案:
$5$
7. 定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰三角形ABC中,∠A = 80°,则它的特征值k = ______.
答案:
$\frac{8}{5}$或$\frac{1}{4}$
8. 等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其底边上的高是______.
答案:
【解析】:本题需要分情况讨论等腰三角形的顶角是锐角还是钝角,再根据三角形内角和定理及等腰三角形的性质求出底边上的高。
- **当等腰三角形为锐角三角形时:**
已知一腰上的高与另一腰的夹角为$30^{\circ}$,因为高与腰形成一个直角三角形,其中一个角为$30^{\circ}$,根据直角三角形两锐角互余,可求出顶角为$90^{\circ}-30^{\circ}=60^{\circ}$。
因为该三角形是等腰三角形且有一个角为$60^{\circ}$,所以这个等腰三角形是等边三角形,即三边都为$6$。
根据等边三角形三线合一的性质,底边上的高将底边平分,再根据勾股定理可求出底边上的高为$\sqrt{6^{2}-3^{2}}=\sqrt{36 - 9}=\sqrt{27}=3\sqrt{3}$。
- **当等腰三角形为钝角三角形时:**
已知一腰上的高与另一腰的夹角为$30^{\circ}$,因为高在三角形外部,所以此时顶角的外角为$90^{\circ}-30^{\circ}=60^{\circ}$,根据邻补角的性质,可求出顶角为$180^{\circ}-60^{\circ}=120^{\circ}$。
因为等腰三角形两底角相等,且三角形内角和为$180^{\circ}$,所以底角为$(180^{\circ}-120^{\circ})\div2 = 30^{\circ}$。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,腰长为$6$,则底边上的高为$\dfrac{1}{2}\times6 = 3$。
综上,其底边上的高是$3$或$3\sqrt{3}$。
【答案】:$3$或$3\sqrt{3}$
- **当等腰三角形为锐角三角形时:**
已知一腰上的高与另一腰的夹角为$30^{\circ}$,因为高与腰形成一个直角三角形,其中一个角为$30^{\circ}$,根据直角三角形两锐角互余,可求出顶角为$90^{\circ}-30^{\circ}=60^{\circ}$。
因为该三角形是等腰三角形且有一个角为$60^{\circ}$,所以这个等腰三角形是等边三角形,即三边都为$6$。
根据等边三角形三线合一的性质,底边上的高将底边平分,再根据勾股定理可求出底边上的高为$\sqrt{6^{2}-3^{2}}=\sqrt{36 - 9}=\sqrt{27}=3\sqrt{3}$。
- **当等腰三角形为钝角三角形时:**
已知一腰上的高与另一腰的夹角为$30^{\circ}$,因为高在三角形外部,所以此时顶角的外角为$90^{\circ}-30^{\circ}=60^{\circ}$,根据邻补角的性质,可求出顶角为$180^{\circ}-60^{\circ}=120^{\circ}$。
因为等腰三角形两底角相等,且三角形内角和为$180^{\circ}$,所以底角为$(180^{\circ}-120^{\circ})\div2 = 30^{\circ}$。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,腰长为$6$,则底边上的高为$\dfrac{1}{2}\times6 = 3$。
综上,其底边上的高是$3$或$3\sqrt{3}$。
【答案】:$3$或$3\sqrt{3}$
9. 如图1 - 30,在△ABC中,∠C = 90°,∠A = 30°,BD平分∠ABC交AC于点D,若CD = 2 cm,则AC = ______ cm.


答案:
1. 首先求$\angle ABC$的度数:
在$\triangle ABC$中,因为$\angle C = 90^{\circ}$,$\angle A = 30^{\circ}$,根据三角形内角和为$180^{\circ}$,即$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle ABC=180^{\circ}-\angle A - \angle C$。
把$\angle A = 30^{\circ}$,$\angle C = 90^{\circ}$代入可得$\angle ABC = 60^{\circ}$。
2. 然后求$\angle ABD$和$\angle DBC$的度数:
因为$BD$平分$\angle ABC$,所以$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC$。
则$\angle ABD=\angle DBC = 30^{\circ}$。
3. 接着求$BD$的长度:
在$Rt\triangle BCD$中,$\angle C = 90^{\circ}$,$\angle DBC = 30^{\circ}$,根据在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半,设$BD=x$,则$CD=\frac{1}{2}BD$($30^{\circ}$角所对直角边是$CD$,斜边是$BD$)。
已知$CD = 2cm$,由$CD=\frac{1}{2}BD$,可得$BD = 4cm$。
4. 最后求$AD$的长度:
因为$\angle A=\angle ABD = 30^{\circ}$,所以$\triangle ABD$是等腰三角形(等角对等边),则$AD = BD$。
所以$AD = 4cm$。
又因为$AC=AD + CD$,$CD = 2cm$,$AD = 4cm$,所以$AC=4 + 2=6cm$。
故答案为$6$。
在$\triangle ABC$中,因为$\angle C = 90^{\circ}$,$\angle A = 30^{\circ}$,根据三角形内角和为$180^{\circ}$,即$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle ABC=180^{\circ}-\angle A - \angle C$。
把$\angle A = 30^{\circ}$,$\angle C = 90^{\circ}$代入可得$\angle ABC = 60^{\circ}$。
2. 然后求$\angle ABD$和$\angle DBC$的度数:
因为$BD$平分$\angle ABC$,所以$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC$。
则$\angle ABD=\angle DBC = 30^{\circ}$。
3. 接着求$BD$的长度:
在$Rt\triangle BCD$中,$\angle C = 90^{\circ}$,$\angle DBC = 30^{\circ}$,根据在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半,设$BD=x$,则$CD=\frac{1}{2}BD$($30^{\circ}$角所对直角边是$CD$,斜边是$BD$)。
已知$CD = 2cm$,由$CD=\frac{1}{2}BD$,可得$BD = 4cm$。
4. 最后求$AD$的长度:
因为$\angle A=\angle ABD = 30^{\circ}$,所以$\triangle ABD$是等腰三角形(等角对等边),则$AD = BD$。
所以$AD = 4cm$。
又因为$AC=AD + CD$,$CD = 2cm$,$AD = 4cm$,所以$AC=4 + 2=6cm$。
故答案为$6$。
10. 如图1 - 31,在△ABC中,∠A = 70°,DO,EO分别为AB,AC的垂直平分线,则∠BOC的度数为______.
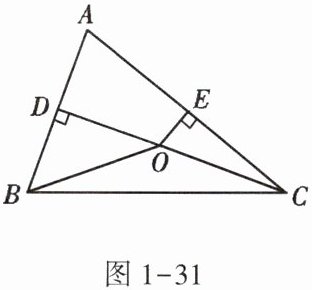

答案:
1. 首先,连接$AO$:
因为$DO$是$AB$的垂直平分线,根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等,所以$OA = OB$,则$\angle OAB=\angle OBA$。
同理,因为$EO$是$AC$的垂直平分线,所以$OA = OC$,则$\angle OAC=\angle OCA$。
2. 然后,求$\angle OBA+\angle OCA$的值:
已知$\angle BAC=\angle OAB + \angle OAC=70^{\circ}$,所以$\angle OBA+\angle OCA=\angle OAB+\angle OAC = 70^{\circ}$。
在$\triangle ABC$中,根据三角形内角和定理$\angle ABC+\angle ACB=180^{\circ}-\angle BAC$,把$\angle BAC = 70^{\circ}$代入可得$\angle ABC+\angle ACB = 180 - 70=110^{\circ}$。
又因为$\angle OBC+\angle OCB=(\angle ABC - \angle OBA)+(\angle ACB-\angle OCA)=(\angle ABC+\angle ACB)-(\angle OBA + \angle OCA)$。
把$\angle ABC+\angle ACB = 110^{\circ}$,$\angle OBA+\angle OCA = 70^{\circ}$代入上式,得$\angle OBC+\angle OCB=110 - 70 = 40^{\circ}$。
3. 最后,求$\angle BOC$的度数:
在$\triangle BOC$中,根据三角形内角和定理$\angle BOC=180^{\circ}-(\angle OBC+\angle OCB)$。
把$\angle OBC+\angle OCB = 40^{\circ}$代入,得$\angle BOC=180 - 40=140^{\circ}$。
所以$\angle BOC$的度数为$140^{\circ}$。
因为$DO$是$AB$的垂直平分线,根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等,所以$OA = OB$,则$\angle OAB=\angle OBA$。
同理,因为$EO$是$AC$的垂直平分线,所以$OA = OC$,则$\angle OAC=\angle OCA$。
2. 然后,求$\angle OBA+\angle OCA$的值:
已知$\angle BAC=\angle OAB + \angle OAC=70^{\circ}$,所以$\angle OBA+\angle OCA=\angle OAB+\angle OAC = 70^{\circ}$。
在$\triangle ABC$中,根据三角形内角和定理$\angle ABC+\angle ACB=180^{\circ}-\angle BAC$,把$\angle BAC = 70^{\circ}$代入可得$\angle ABC+\angle ACB = 180 - 70=110^{\circ}$。
又因为$\angle OBC+\angle OCB=(\angle ABC - \angle OBA)+(\angle ACB-\angle OCA)=(\angle ABC+\angle ACB)-(\angle OBA + \angle OCA)$。
把$\angle ABC+\angle ACB = 110^{\circ}$,$\angle OBA+\angle OCA = 70^{\circ}$代入上式,得$\angle OBC+\angle OCB=110 - 70 = 40^{\circ}$。
3. 最后,求$\angle BOC$的度数:
在$\triangle BOC$中,根据三角形内角和定理$\angle BOC=180^{\circ}-(\angle OBC+\angle OCB)$。
把$\angle OBC+\angle OCB = 40^{\circ}$代入,得$\angle BOC=180 - 40=140^{\circ}$。
所以$\angle BOC$的度数为$140^{\circ}$。
查看更多完整答案,请扫码查看


