《2025年暑假作业本大象出版社八年级数学北师大版》

4. 已知∠MAN = 120°，AC平分∠MAN，点B，D分别在AN，AM上.
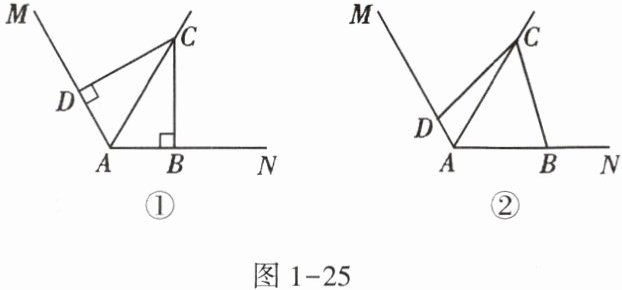
（1）如图1 - 25①，若∠ABC = ∠ADC = 90°，请你探索线段AD，AB，AC之间的数量关系，并证明.
（2）如图1 - 25②，若∠ABC + ∠ADC = 180°，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由.

答案： 【解析】：
（1）
因为$AC$平分$\angle MAN$，$\angle MAN = 120^{\circ}$，所以$\angle CAD=\angle CAB = 60^{\circ}$。
在$Rt\triangle ADC$中，$\angle ACD = 30^{\circ}$，则$AC = 2AD$；在$Rt\triangle ABC$中，$\angle ACB = 30^{\circ}$，则$AC = 2AB$。
所以$AD + AB=\frac{1}{2}AC+\frac{1}{2}AC = AC$。
（2）
过点$C$分别作$CE\perp AM$于点$E$，$CF\perp AN$于点$F$。
因为$AC$平分$\angle MAN$，所以$CE = CF$。
因为$\angle ABC+\angle ADC = 180^{\circ}$，$\angle ADC+\angle CDE = 180^{\circ}$，所以$\angle CDE=\angle ABC$。
又$\angle CED=\angle CFB = 90^{\circ}$，所以$\triangle CDE\cong\triangle CBF(AAS)$，则$DE = BF$。
在$Rt\triangle ACE$中，$\angle CAE = 60^{\circ}$，$\angle ACE = 30^{\circ}$，所以$AC = 2AE$；同理$AC = 2AF$。
$AE=AD + DE$，$AF = AB - BF$，又$DE = BF$，所以$AE+AF=(AD + DE)+(AB - BF)=AD + AB$。
而$AE + AF=\frac{1}{2}AC+\frac{1}{2}AC = AC$，所以$AD + AB = AC$，结论仍然成立。
【答案】：
（1）$AD + AB = AC$；（2）成立

1. 到三角形三个顶点的距离相等的点是三角形______的交点（ ）

答案： B

2. 已知△ABC的三边长分别是6 cm，8 cm，10 cm，则△ABC的面积是（ ）
A. 24 cm²
B. 30 cm²
C. 40 cm²
D. 48 cm²

答案： A

3. 如图1 - 26，在△ABC和△DEF中，已知AC = DF，BC = EF，要使△ABC≌△DEF，还需要的条件是（ ）

A. ∠A = ∠D
B. ∠ACB = ∠F
C. ∠B = ∠DEF
D. ∠ACB = ∠D

答案： B