第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
项目式学习
解密领奖台的表面积之谜
任务1 准备领奖台模型材料
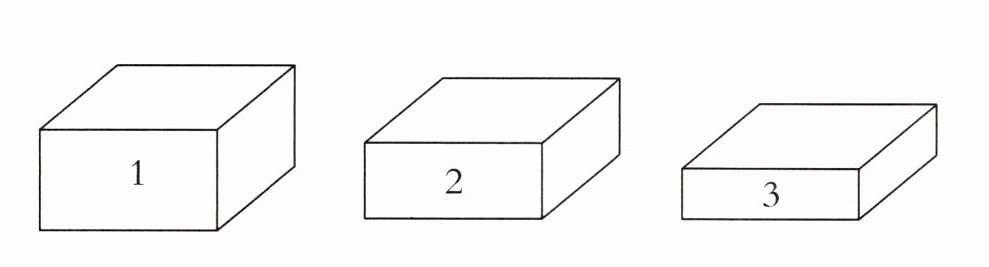
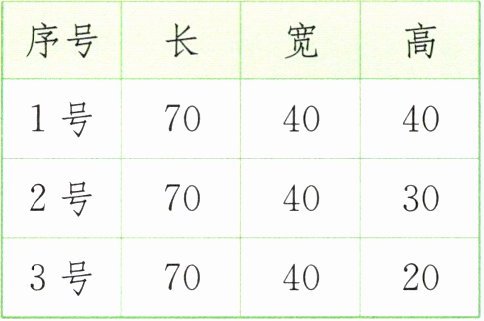
用3个底面相同、高不相等的长方体(如下图)模拟领奖台。下表记录的是三个长方体的长、宽、高。(单位:厘米)
任务2 制作彩色领奖台模型
步骤1: 如图,把1号、2号、3号三个不同的长方体按领奖台的位置摆放。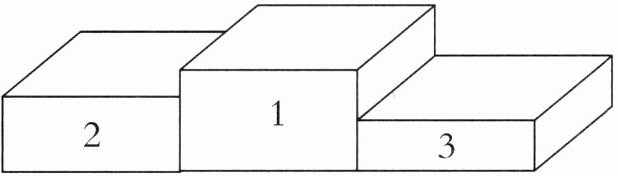
步骤2: 在拼好的领奖台表面涂上颜色。
任务3 解决实际问题
问题1: 这三个长方体的表面积分别是多少平方分米?
1号长方体表面积是
问题2: 这个领奖台表面涂色部分的面积是多少平方分米?
领奖台表面涂色部分的面积是
我的思考
这个领奖台的表面涂色部分的面积是指哪些面的面积呢?
底面和遮挡的面都没有涂色,是否要计入表面积呢?
我的解答
解密领奖台的表面积之谜
任务1 准备领奖台模型材料
用3个底面相同、高不相等的长方体(如下图)模拟领奖台。下表记录的是三个长方体的长、宽、高。(单位:厘米)


任务2 制作彩色领奖台模型
步骤1: 如图,把1号、2号、3号三个不同的长方体按领奖台的位置摆放。

步骤2: 在拼好的领奖台表面涂上颜色。
任务3 解决实际问题
问题1: 这三个长方体的表面积分别是多少平方分米?
1号长方体表面积是
144
平方分米,2号长方体表面积是122
平方分米,3号长方体表面积是100
平方分米。问题2: 这个领奖台表面涂色部分的面积是多少平方分米?
领奖台表面涂色部分的面积是
256
平方分米。我的思考
这个领奖台的表面涂色部分的面积是指哪些面的面积呢?
底面和遮挡的面都没有涂色,是否要计入表面积呢?
我的解答
答案:
【解析】:
### 问题1:计算三个长方体的表面积
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),同时注意单位换算($1$平方分米$ = 100$平方厘米)。
**1号长方体**:
$S_1=(70×40 + 70×40 + 40×40)×2$
$=(2800+2800 + 1600)×2$
$=(5600+1600)×2$
$=7200×2=14400$(平方厘米)
$14400$平方厘米$=14400÷100 = 144$平方分米。
**2号长方体**:
$S_2=(70×40 + 70×30 + 40×30)×2$
$=(2800+2100 + 1200)×2$
$=(4900+1200)×2$
$=6100×2 = 12200$(平方厘米)
$12200$平方厘米$=12200÷100=122$平方分米。
**3号长方体**:
$S_3=(70×40 + 70×20 + 40×20)×2$
$=(2800+1400 + 800)×2$
$=(4200+800)×2$
$=5000×2=10000$(平方厘米)
$10000$平方厘米$=10000÷100 = 100$平方分米。
### 问题2:计算领奖台表面涂色部分的面积
通过平移法,领奖台表面涂色部分的面积可以看作是一个大长方体的表面积(长$70$厘米、宽$(40×3)$厘米、高$40$厘米)减去$4$个$40×40$的正方形面积(遮挡部分)。
先计算大长方体表面积$S=(70×(40×3)+70×40+(40×3)×40)×2$
$=(70×120 + 2800+120×40)×2$
$=(8400+2800 + 4800)×2$
$=(11200+4800)×2$
$=16000×2=32000$(平方厘米)
再计算$4$个$40×40$正方形面积$4×40×40 = 6400$(平方厘米)
则领奖台表面涂色部分面积$S_{涂}=32000-6400=25600$(平方厘米)
$25600$平方厘米$=25600÷100 = 256$平方分米。
【答案】:
问题1:1号长方体表面积是$\boldsymbol{144}$平方分米,2号长方体表面积是$\boldsymbol{122}$平方分米,3号长方体表面积是$\boldsymbol{100}$平方分米。
问题2:领奖台表面涂色部分的面积是$\boldsymbol{256}$平方分米。
### 问题1:计算三个长方体的表面积
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),同时注意单位换算($1$平方分米$ = 100$平方厘米)。
**1号长方体**:
$S_1=(70×40 + 70×40 + 40×40)×2$
$=(2800+2800 + 1600)×2$
$=(5600+1600)×2$
$=7200×2=14400$(平方厘米)
$14400$平方厘米$=14400÷100 = 144$平方分米。
**2号长方体**:
$S_2=(70×40 + 70×30 + 40×30)×2$
$=(2800+2100 + 1200)×2$
$=(4900+1200)×2$
$=6100×2 = 12200$(平方厘米)
$12200$平方厘米$=12200÷100=122$平方分米。
**3号长方体**:
$S_3=(70×40 + 70×20 + 40×20)×2$
$=(2800+1400 + 800)×2$
$=(4200+800)×2$
$=5000×2=10000$(平方厘米)
$10000$平方厘米$=10000÷100 = 100$平方分米。
### 问题2:计算领奖台表面涂色部分的面积
通过平移法,领奖台表面涂色部分的面积可以看作是一个大长方体的表面积(长$70$厘米、宽$(40×3)$厘米、高$40$厘米)减去$4$个$40×40$的正方形面积(遮挡部分)。
先计算大长方体表面积$S=(70×(40×3)+70×40+(40×3)×40)×2$
$=(70×120 + 2800+120×40)×2$
$=(8400+2800 + 4800)×2$
$=(11200+4800)×2$
$=16000×2=32000$(平方厘米)
再计算$4$个$40×40$正方形面积$4×40×40 = 6400$(平方厘米)
则领奖台表面涂色部分面积$S_{涂}=32000-6400=25600$(平方厘米)
$25600$平方厘米$=25600÷100 = 256$平方分米。
【答案】:
问题1:1号长方体表面积是$\boldsymbol{144}$平方分米,2号长方体表面积是$\boldsymbol{122}$平方分米,3号长方体表面积是$\boldsymbol{100}$平方分米。
问题2:领奖台表面涂色部分的面积是$\boldsymbol{256}$平方分米。
查看更多完整答案,请扫码查看


