2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 如图,在△ABC中,∠B = 60°,∠C = 40°,AD和AE分别是它的高和角平分线,那么∠DAE的度数是______.
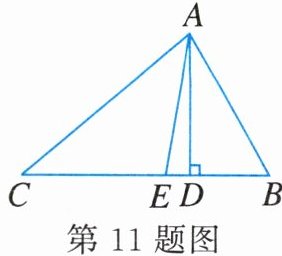

答案:
$10^{\circ}$
12. 如图,在△ABC中,已知点D为BC上一点,E,F分别为AD,BE的中点,且$S_{△ABC} = 8 cm^2,$则图中阴影部分△CEF的面积是______cm^2.
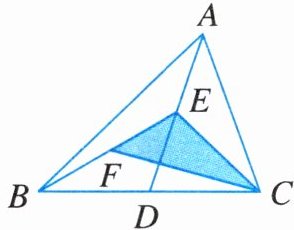

答案:
2
13. 如图,在△ABC(∠BAC = 90°)中,AE⊥BC,垂足为点E,D是边BC上的一点,连结AD.
(1)写出△ABE的三个内角;
(2)在△ABD中,∠B的对边是______;在△ABC中,∠B的对边是______;
(3)图中的三角形中,哪些是直角三角形?哪些是锐角三角形?哪些是钝角三角形?
(4)线段AD是哪些三角形的公共边?
(5)∠ADC和∠AED分别是哪些三角形的公共角?
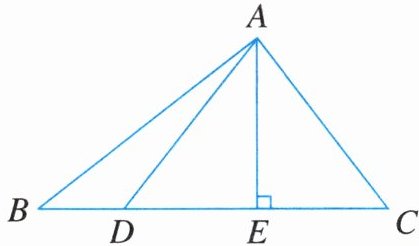
(1)写出△ABE的三个内角;
(2)在△ABD中,∠B的对边是______;在△ABC中,∠B的对边是______;
(3)图中的三角形中,哪些是直角三角形?哪些是锐角三角形?哪些是钝角三角形?
(4)线段AD是哪些三角形的公共边?
(5)∠ADC和∠AED分别是哪些三角形的公共角?

答案:
(1) $\angle BAE$,$\angle B$,$\angle AEB$
(2) $AD$ $AC$
(3) 直角三角形是$\triangle ABE$,$\triangle ADE$,$\triangle AEC$,$\triangle BAC$;锐角三角形是$\triangle ADC$;钝角三角形是$\triangle ABD$。
(4) 线段$AD$是$\triangle ABD$,$\triangle ADE$,$\triangle ADC$的公共边。
(5) $\angle ADC$是$\triangle ADE$,$\triangle ADC$的公共角;$\angle AED$是$\triangle ABE$,$\triangle ADE$的公共角。
(1) $\angle BAE$,$\angle B$,$\angle AEB$
(2) $AD$ $AC$
(3) 直角三角形是$\triangle ABE$,$\triangle ADE$,$\triangle AEC$,$\triangle BAC$;锐角三角形是$\triangle ADC$;钝角三角形是$\triangle ABD$。
(4) 线段$AD$是$\triangle ABD$,$\triangle ADE$,$\triangle ADC$的公共边。
(5) $\angle ADC$是$\triangle ADE$,$\triangle ADC$的公共角;$\angle AED$是$\triangle ABE$,$\triangle ADE$的公共角。
14. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5 cm,AB与AC的和为13 cm,求AC的长.
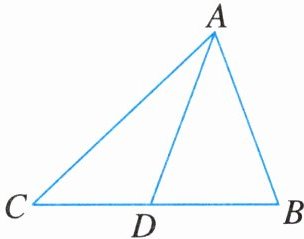

答案:
$\because AD$是$BC$边上的中线,$\therefore D$为$BC$的中点,$CD = BD$。$\because \triangle ADC$的周长$- \triangle ABD$的周长$= 5 cm$,$\therefore AC - AB = 5 cm$。又$\because AB + AC = 13 cm$,$\therefore AC = 9 cm$。
15. 如图,在△ABC中,AD是BC边上的高,AE是角平分线,∠B = 20°,∠C = 60°.
(1)求∠CAD,∠AEC和∠EAD的度数;
(2)若图形发生了变化,当∠B = 30°,∠C = 60°时,则∠EAD = ______°;当∠C - ∠B = 10°时,则∠EAD = ______°;
(3)若∠B和∠C的度数分别用字母α和β来表示,你能找到∠EAD与α和β之间的关系吗?请直接写出你发现的结论.

(1)求∠CAD,∠AEC和∠EAD的度数;
(2)若图形发生了变化,当∠B = 30°,∠C = 60°时,则∠EAD = ______°;当∠C - ∠B = 10°时,则∠EAD = ______°;
(3)若∠B和∠C的度数分别用字母α和β来表示,你能找到∠EAD与α和β之间的关系吗?请直接写出你发现的结论.

答案:
(1) $\because \angle B = 20^{\circ}$,$\angle C = 60^{\circ}$,$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 100^{\circ}$。$\because AE$平分$\angle BAC$,$\therefore \angle BAE = \angle EAC = \frac{1}{2}\angle BAC = 50^{\circ}$。$\therefore \angle AEB = 180^{\circ} - \angle BAE - \angle B = 110^{\circ}$。$\therefore \angle AEC = 180^{\circ} - \angle AEB = 70^{\circ}$。$\because AD$是$BC$边上的高,$\therefore \angle ADC = 90^{\circ}$。$\therefore \angle CAD = 180^{\circ} - \angle ADC - \angle C = 30^{\circ}$。$\therefore \angle EAD = \angle EAC - \angle CAD = 20^{\circ}$。综上所述,$\angle CAD = 30^{\circ}$,$\angle AEC = 70^{\circ}$,$\angle EAD = 20^{\circ}$。
(2) 易得$\angle EAD = \angle EAC - \angle CAD = \frac{1}{2}\angle BAC - \angle CAD = \frac{1}{2}[180^{\circ} - (\angle B + \angle C)] - (180^{\circ} - \angle ADC - \angle C) = \frac{1}{2}(\angle C - \angle B)$,$\therefore$当$\angle B = 30^{\circ}$,$\angle C = 60^{\circ}$时,$\angle EAD = 15^{\circ}$;当$\angle C - \angle B = 10^{\circ}$时,$\angle EAD = 5^{\circ}$。
(3) 当$\alpha < \beta$时,$\angle EAD = \frac{1}{2}(\beta - \alpha)$;当$\alpha > \beta$时,$\angle EAD = \frac{1}{2}(\alpha - \beta)$。
(1) $\because \angle B = 20^{\circ}$,$\angle C = 60^{\circ}$,$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 100^{\circ}$。$\because AE$平分$\angle BAC$,$\therefore \angle BAE = \angle EAC = \frac{1}{2}\angle BAC = 50^{\circ}$。$\therefore \angle AEB = 180^{\circ} - \angle BAE - \angle B = 110^{\circ}$。$\therefore \angle AEC = 180^{\circ} - \angle AEB = 70^{\circ}$。$\because AD$是$BC$边上的高,$\therefore \angle ADC = 90^{\circ}$。$\therefore \angle CAD = 180^{\circ} - \angle ADC - \angle C = 30^{\circ}$。$\therefore \angle EAD = \angle EAC - \angle CAD = 20^{\circ}$。综上所述,$\angle CAD = 30^{\circ}$,$\angle AEC = 70^{\circ}$,$\angle EAD = 20^{\circ}$。
(2) 易得$\angle EAD = \angle EAC - \angle CAD = \frac{1}{2}\angle BAC - \angle CAD = \frac{1}{2}[180^{\circ} - (\angle B + \angle C)] - (180^{\circ} - \angle ADC - \angle C) = \frac{1}{2}(\angle C - \angle B)$,$\therefore$当$\angle B = 30^{\circ}$,$\angle C = 60^{\circ}$时,$\angle EAD = 15^{\circ}$;当$\angle C - \angle B = 10^{\circ}$时,$\angle EAD = 5^{\circ}$。
(3) 当$\alpha < \beta$时,$\angle EAD = \frac{1}{2}(\beta - \alpha)$;当$\alpha > \beta$时,$\angle EAD = \frac{1}{2}(\alpha - \beta)$。
查看更多完整答案,请扫码查看


