《2025年第三学期暑假衔接七年级数学浙教版》

14. 小伟同学的作业本上有一道练习题,这道题被除式的第二项和商的第一项不小心被墨水覆盖(覆盖处用字母$M和N$表示):
$(30x^{4}y^{2}+M+12x^{2}y^{2})÷(-6x^{2}y)= N+3xy-2y$.
(1)请你帮小伟复原被覆盖的代数式$M和N$;
(2)小伟在进一步练习时将复原后的$N+3xy-2y与代数式x^{2}y+xy+y$相加,请帮他求出这两个代数式的和,并判断所求的和能否进行因式分解.若能,请分解因式;若不能,请说明理由.

答案： 14.
(1) $N = - 5x^2y$，$M = - 18x^3y^2$
(2) 和为 $- 4x^2y + 4xy - y$，能够因式分解，$- y(2x - 1)^2$

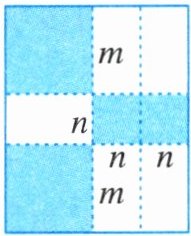
15. 如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为$m$的大正方形,两块是边长都为$n$的小正方形,五块是长为$m$、宽为$n$的小长方形,且$m＞n$. (以上长度单位:cm)
(1)观察图形,可以发现代数式$2m^{2}+5mn+2n^{2}$可以因式分解为______;
(2)若每块小长方形的面积为$20cm^{2}$,四个正方形的面积和为$162cm^{2}$.
①试求图中所有裁剪线(虚线部分)的长度之和;②求$(m-n)^{2}$的值.

答案： 15.
(1) $(2m + n)(m + 2n)$
(2) ① 由题意知，$mn = 20$，$2m^2 + 2n^2 = 162$，解得 $m^2 + n^2 = 81$，$nm = 20$，$\therefore (m + n)^2 = m^2 + n^2 + 2mn = 121$，$\therefore m + n = 11$。图中所有裁剪线(虚线部分)长度之和为 $6(m + n) = 66(cm)$。② $(m - n)^2 = m^2 + n^2 - 2mn = 81 - 40 = 41$。