2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图,将三角形ABC沿AB方向平移到三角形BDE的位置.若$∠CAB= 50^{\circ}$,$∠ABC= 100^{\circ}$,则$∠1= $______.
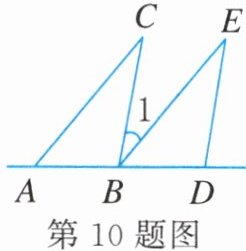

答案:
$30^{\circ}$
11. 如图,将直径为2cm的圆$O_{1}$平移3cm到圆$O_{2}$的位置,则图中阴影部分的面积为______$cm^{2}$.
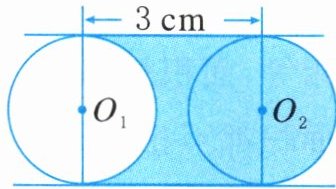

答案:
6
12. 大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如右图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为$t$秒,两个正方形重叠部分的面积为$S$平方厘米。当$S= 2$时,小正方形平移的时间为______秒.
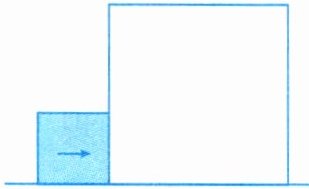

答案:
1 或 6
13. 在下图所示的$4×4$方格中,按下列要求作格点三角形.(图形的顶点都在正方形格纸的格点上)
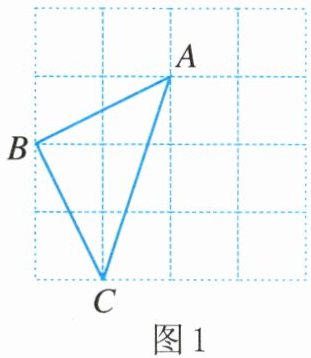
(1)在图1中,将$\triangle ABC$平移,得到$\triangle A'B'C'$,使得$\triangle A'B'C'与\triangle ABC$无重合部分;
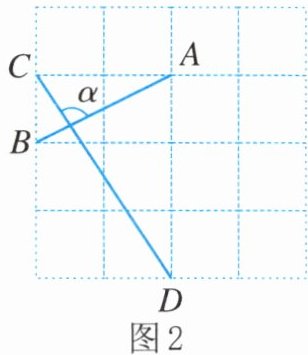
(2)在图2中,线段AB与CD相交,产生$∠α$,请画一个$\triangle ABE$,使得$\triangle ABE中的一个角等于∠α$.


(1)在图1中,将$\triangle ABC$平移,得到$\triangle A'B'C'$,使得$\triangle A'B'C'与\triangle ABC$无重合部分;
(2)在图2中,线段AB与CD相交,产生$∠α$,请画一个$\triangle ABE$,使得$\triangle ABE中的一个角等于∠α$.
答案:
本题可根据平移的性质和作一个角等于已知角的方法进行作图。
$(1)$ 平移$\triangle ABC$
平移的性质:平移不改变图形的形状和大小,经过平移,对应线段平行(或共线)且相等,对应角相等 ,对应点所连接的线段平行且相等。
根据平移的性质,将$\triangle ABC$向右平移$2$个单位,再向上平移$1$个单位(平移方式不唯一),得到$\triangle A'B'C'$,此时$\triangle A'B'C'$与$\triangle ABC$无重合部分。
$(2)$ 作$\triangle ABE$,使其中一个角等于$\angle\alpha$
根据作一个角等于已知角的方法(利用全等三角形的性质,通过构造相等的边来得到相等的角):
以$A$为顶点,$AB$为一边,在$AB$的上方作$\angle BAE=\angle\alpha$,在$AE$上取一点$E$($E$为格点),连接$BE$,则$\triangle ABE$即为所求(答案不唯一)。
综上,$(1)$ 按上述平移方法作图(答案不唯一);$(2)$ 按上述作角方法作图(答案不唯一)。
$(1)$ 平移$\triangle ABC$
平移的性质:平移不改变图形的形状和大小,经过平移,对应线段平行(或共线)且相等,对应角相等 ,对应点所连接的线段平行且相等。
根据平移的性质,将$\triangle ABC$向右平移$2$个单位,再向上平移$1$个单位(平移方式不唯一),得到$\triangle A'B'C'$,此时$\triangle A'B'C'$与$\triangle ABC$无重合部分。
$(2)$ 作$\triangle ABE$,使其中一个角等于$\angle\alpha$
根据作一个角等于已知角的方法(利用全等三角形的性质,通过构造相等的边来得到相等的角):
以$A$为顶点,$AB$为一边,在$AB$的上方作$\angle BAE=\angle\alpha$,在$AE$上取一点$E$($E$为格点),连接$BE$,则$\triangle ABE$即为所求(答案不唯一)。
综上,$(1)$ 按上述平移方法作图(答案不唯一);$(2)$ 按上述作角方法作图(答案不唯一)。
14. 如图,A,B两地之间有一条小河,现在想在河岸搭一座桥(桥与河岸垂直),要使从点A处过桥到点B处的路程最短,应搭在什么地方?请在图中画出示意图.
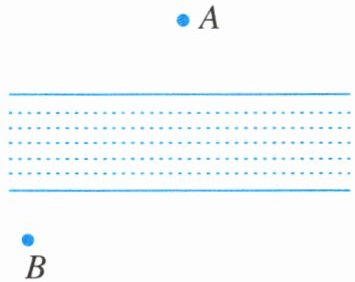

答案:
【解析】:
1. 首先,过点$A$作河岸的垂线$AA'$,使$AA'$等于河宽(两平行线间的距离)。
2. 然后,连接$A'B$,与靠近$B$点的河岸交于点$C$。
3. 最后,过点$C$作河岸的垂线交另一条河岸于点$D$,$CD$就是所搭的桥。
理由:因为$AA' // CD$且$AA' = CD$,所以四边形$AA'CD$是平行四边形,$AD = A'C$。那么$AD + DB = A'C + DB = A'B$,根据两点之间线段最短,此时从$A$过桥到$B$的路程最短。
【答案】:过点$A$作河岸垂线$AA'$($AA'$等于河宽),连接$A'B$交靠近$B$的河岸于$C$,过$C$作河岸垂线交另一河岸于$D$,$CD$为桥的位置(按上述步骤画图)。
1. 首先,过点$A$作河岸的垂线$AA'$,使$AA'$等于河宽(两平行线间的距离)。
2. 然后,连接$A'B$,与靠近$B$点的河岸交于点$C$。
3. 最后,过点$C$作河岸的垂线交另一条河岸于点$D$,$CD$就是所搭的桥。
理由:因为$AA' // CD$且$AA' = CD$,所以四边形$AA'CD$是平行四边形,$AD = A'C$。那么$AD + DB = A'C + DB = A'B$,根据两点之间线段最短,此时从$A$过桥到$B$的路程最短。
【答案】:过点$A$作河岸垂线$AA'$($AA'$等于河宽),连接$A'B$交靠近$B$的河岸于$C$,过$C$作河岸垂线交另一河岸于$D$,$CD$为桥的位置(按上述步骤画图)。
15. 如图,将直角三角形ABC沿BC方向平移到三角形DEF的位置,$AB= 10$,$DH= 4$,平移距离为6,求阴影部分的面积.
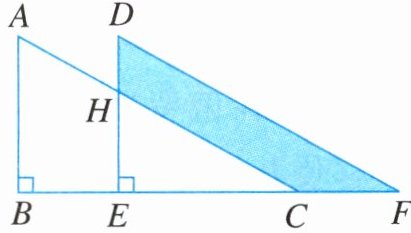

答案:
48
查看更多完整答案,请扫码查看


