2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
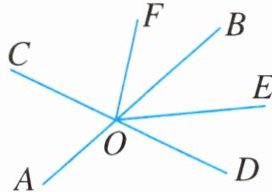
10. 如图,直线 $ AB $,$ CD $ 相交于点 $ O $,$ OE $ 平分 $ \angle BOD $,$ OF $ 平分 $ \angle COE $。若 $ \angle AOC $ 的度数为 $ 2 \alpha $,则 $ \angle EOF = $______。(用含 $ \alpha $ 的代数式表示)

答案:
$90^{\circ}-\frac{\alpha}{2}$
11. 两条直线被第三条直线所截,如果一对同位角相等,那么内错角也相等,同旁内角互补。试将下列说理过程补充完整。
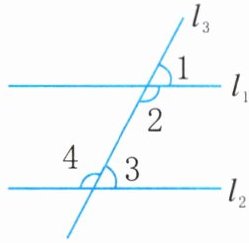
解:如图,设 $ \angle 1 = \angle 3 $。
$ \because \angle 1 + \angle 2 = $______$ ^ { \circ } $(平角的定义),
$ \therefore \angle 3 + $______$ = 180 ^ { \circ } $。
又 $ \because \angle 4 + \angle 3 = $______$ ^ { \circ } $(平角的定义),
$ \therefore \angle 2 = \angle 4 $(______)。

解:如图,设 $ \angle 1 = \angle 3 $。
$ \because \angle 1 + \angle 2 = $______$ ^ { \circ } $(平角的定义),
$ \therefore \angle 3 + $______$ = 180 ^ { \circ } $。
又 $ \because \angle 4 + \angle 3 = $______$ ^ { \circ } $(平角的定义),
$ \therefore \angle 2 = \angle 4 $(______)。
答案:
180 $∠2$ 180 同角的补角相等
12. 如图,与 $ \angle A $ 是同旁内角的角共有______个。

答案:
4
13. 如图,直线 $ AB $,$ CD $ 相交于点 $ O $,$ \angle BOD $ 和 $ \angle AON $ 互余,$ \angle AON = \angle COM $。
(1)求 $ \angle MOB $ 的度数;
(2)若 $ \angle COM = \frac { 1 } { 5 } \angle BOC $,求 $ \angle BOD $ 的度数。
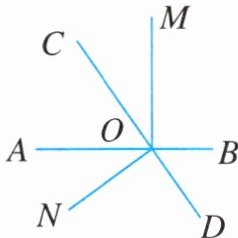
(1)求 $ \angle MOB $ 的度数;
(2)若 $ \angle COM = \frac { 1 } { 5 } \angle BOC $,求 $ \angle BOD $ 的度数。

答案:
(1)$90^{\circ}$
(2)$67.5^{\circ}$
(1)$90^{\circ}$
(2)$67.5^{\circ}$
14. 如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来。
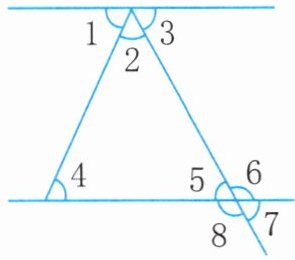

答案:
同位角为$∠3$与$∠7$,$∠2$与$∠8$,$∠4$与$∠6$。内错角为$∠1$与$∠4$,$∠3$与$∠5$,$∠2$与$∠6$,$∠4$与$∠8$。同旁内角为$∠3$与$∠6$,$∠2$与$∠5$,$∠2$与$∠4$,$∠4$与$∠5$。
15. 如图所示的是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角。跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置 $ \angle 1 $ 跳到终点位置 $ \angle 3 $,写出其中两种不同路径:
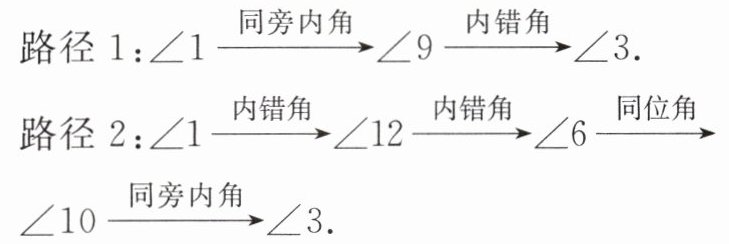
试一试:
(1)从起始角 $ \angle 1 $ 跳到终点角 $ \angle 8 $;
(2)从起始角 $ \angle 1 $ 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角 $ \angle 8 $?
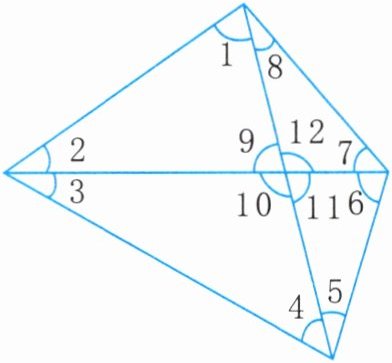

试一试:
(1)从起始角 $ \angle 1 $ 跳到终点角 $ \angle 8 $;
(2)从起始角 $ \angle 1 $ 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角 $ \angle 8 $?

答案:
(1)路径:$∠1\xrightarrow{内错角}∠12\xrightarrow{同旁内角}∠8$。
(2)从起始角$∠1$依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角$∠8$。其路径为$∠1\xrightarrow{同位角}∠10\xrightarrow{内错角}∠5\xrightarrow{同旁内角}∠8$。
(1)路径:$∠1\xrightarrow{内错角}∠12\xrightarrow{同旁内角}∠8$。
(2)从起始角$∠1$依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角$∠8$。其路径为$∠1\xrightarrow{同位角}∠10\xrightarrow{内错角}∠5\xrightarrow{同旁内角}∠8$。
查看更多完整答案,请扫码查看


