2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 如图,$∠A = 60^{\circ}$,$O是AB$上一点,直线$OD与AB的夹角∠BOD = 82^{\circ}$,要使$OD// AC$,则直线$OD绕点O$按逆时针方向至少要旋转______度.
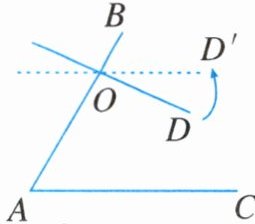

答案:
22
12. 如图,$∠BAM = 75^{\circ}$,$∠BGE = 75^{\circ}$,$∠CHG = 105^{\circ}$,则可推出$AM// EF$,$AB// CD$.完成下面的推理过程(填空).
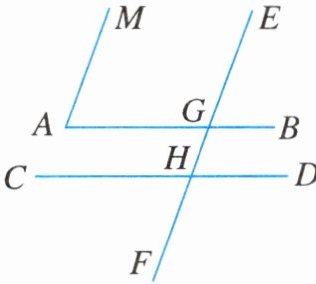
解:$\because ∠BAM = 75^{\circ}$,$∠BGE = 75^{\circ}$(已知),
$\therefore ∠BAM = ∠BGE$,
$\therefore$______$//$______(同位角相等,两直线平行).
$\because ∠AGH = ∠BGE$(对顶角相等),
$\therefore ∠AGH = 75^{\circ}$,
$\therefore ∠AGH + ∠CHG = 75^{\circ} + 105^{\circ} = 180^{\circ}$,
$\therefore$______$//$______(______)

解:$\because ∠BAM = 75^{\circ}$,$∠BGE = 75^{\circ}$(已知),
$\therefore ∠BAM = ∠BGE$,
$\therefore$______$//$______(同位角相等,两直线平行).
$\because ∠AGH = ∠BGE$(对顶角相等),
$\therefore ∠AGH = 75^{\circ}$,
$\therefore ∠AGH + ∠CHG = 75^{\circ} + 105^{\circ} = 180^{\circ}$,
$\therefore$______$//$______(______)
答案:
AM EF AB CD 同旁内角互补,两直线平行
13. 如图,直线$AB$,$CD相交于点O$,$OD平分∠EOB$,$OF平分∠AOE$,$GH⊥CD$,垂足为点$H$,$GH与FO$平行吗?说明理由.
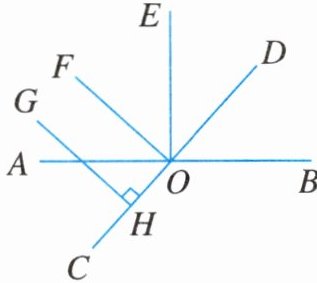

答案:
$GH // FO$。理由:
∵ OD 平分 $\angle EOB$,OF 平分 $\angle AOE$,
∴ $\angle EOD = \frac{1}{2} \angle EOB$,$\angle EOF = \frac{1}{2} \angle AOE$。
∵ $\angle AOE + \angle EOB = 180^{\circ}$,
∴ $\angle EOD + \angle EOF = 90^{\circ}$,即 $\angle DOF = 90^{\circ}$。
∵ $GH \perp CD$,
∴ $\angle GHD = 90^{\circ}$。
∴ $\angle DOF = \angle GHD$。
∴ $GH // FO$。
∵ OD 平分 $\angle EOB$,OF 平分 $\angle AOE$,
∴ $\angle EOD = \frac{1}{2} \angle EOB$,$\angle EOF = \frac{1}{2} \angle AOE$。
∵ $\angle AOE + \angle EOB = 180^{\circ}$,
∴ $\angle EOD + \angle EOF = 90^{\circ}$,即 $\angle DOF = 90^{\circ}$。
∵ $GH \perp CD$,
∴ $\angle GHD = 90^{\circ}$。
∴ $\angle DOF = \angle GHD$。
∴ $GH // FO$。
14. 如图,已知点$E在BD$上,$EA平分∠BEF$,$EC平分∠DEF$.
(1)试说明:$AE⊥CE$;
(2)若$∠1 = ∠A$,$∠4 = ∠C$,则$AB与CD$平行吗?为什么?
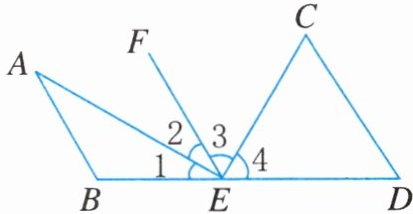
(1)试说明:$AE⊥CE$;
(2)若$∠1 = ∠A$,$∠4 = ∠C$,则$AB与CD$平行吗?为什么?

答案:
(1)
∵ EA 平分 $\angle BEF$,EC 平分 $\angle DEF$,
∴ $\angle 2 = \angle 1 = \frac{1}{2} \angle BEF$,$\angle 3 = \angle 4 = \frac{1}{2} \angle DEF$。
∵ $\angle BEF + \angle DEF = 180^{\circ}$,
∴ $\angle 2 + \angle 3 = \frac{1}{2} (\angle BEF + \angle DEF) = 90^{\circ}$,
∴ $AE \perp CE$。
(2) $AB // CD$。理由:由
(1),得 $\angle 2 = \angle 1$,$\angle 3 = \angle 4$。又
∵ $\angle 1 = \angle A$,$\angle 4 = \angle C$,
∴ $\angle A = \angle 2$,$\angle 3 = \angle C$,
∴ $AB // EF$,$EF // CD$,
∴ $AB // CD$。
(1)
∵ EA 平分 $\angle BEF$,EC 平分 $\angle DEF$,
∴ $\angle 2 = \angle 1 = \frac{1}{2} \angle BEF$,$\angle 3 = \angle 4 = \frac{1}{2} \angle DEF$。
∵ $\angle BEF + \angle DEF = 180^{\circ}$,
∴ $\angle 2 + \angle 3 = \frac{1}{2} (\angle BEF + \angle DEF) = 90^{\circ}$,
∴ $AE \perp CE$。
(2) $AB // CD$。理由:由
(1),得 $\angle 2 = \angle 1$,$\angle 3 = \angle 4$。又
∵ $\angle 1 = \angle A$,$\angle 4 = \angle C$,
∴ $\angle A = \angle 2$,$\angle 3 = \angle C$,
∴ $AB // EF$,$EF // CD$,
∴ $AB // CD$。
15. (1)如图1,$AB$,$CD$,$EF$是三条公路,且$AB⊥EF$,$CD⊥EF$.判断$AB与CD$的位置关系,并说明理由;
(2)如图2,在(1)的条件下,若小路$OM平分∠EOB$,通往加油站$N的岔道O'N平分∠CO'F$,试判断$OM与O'N$的位置关系,并说明理由.
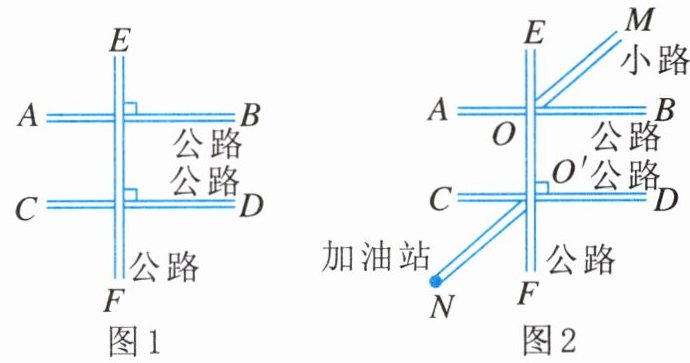
(2)如图2,在(1)的条件下,若小路$OM平分∠EOB$,通往加油站$N的岔道O'N平分∠CO'F$,试判断$OM与O'N$的位置关系,并说明理由.

答案:
(1)
∵ $AB \perp EF$,$CD \perp EF$,
∴ $AB // CD$(同一平面内,垂直于同一直线的两条直线互相平行)。
(2) 延长 $NO'$ 交 AB 于点 P。
∵ OM 平分 $\angle EOB$,$O'N$ 平分 $\angle CO'F$,
∴ $\angle EOM = \angle FO'N = 45^{\circ}$。
∵ $\angle FO'N = \angle EO'P$,
∴ $\angle EOM$
$= \angle EO'P = 45^{\circ}$。
∴ $OM // O'N$(同位角相等,两直线平行)。
(1)
∵ $AB \perp EF$,$CD \perp EF$,
∴ $AB // CD$(同一平面内,垂直于同一直线的两条直线互相平行)。
(2) 延长 $NO'$ 交 AB 于点 P。
∵ OM 平分 $\angle EOB$,$O'N$ 平分 $\angle CO'F$,
∴ $\angle EOM = \angle FO'N = 45^{\circ}$。
∵ $\angle FO'N = \angle EO'P$,
∴ $\angle EOM$
$= \angle EO'P = 45^{\circ}$。
∴ $OM // O'N$(同位角相等,两直线平行)。
查看更多完整答案,请扫码查看


