《2025年第三学期暑假衔接七年级数学浙教版》

14. 在学习用乘法公式分解因式时,我们知道把多项式$a^{2}+2ab+b^{2}及a^{2}-2ab+b^{2}$叫作“完全平方式”。杨老师布置了一道思维拓展题:代数式$x^{2}+2x+5$有最大值还是最小值? 并求出这个最值.小宋的解题步骤如下:
$x^{2}+2x+5$
$=x^{2}+2x+1+4$
$=(x+1)^{2}+4$.
$\because (x+1)^{2}≥0$,
$\therefore (x+1)^{2}+4≥4$,
$\therefore x^{2}+2x+5$的最小值为4.
小宋的解法及结果得到了杨老师的肯定,请根据上述内容完成以下问题:
(1)下列多项式中①$x^{2}+2x-1$;②$x^{2}-6x+9$;③$x^{2}+\frac{1}{2}x+\frac{1}{4}$;④$4y^{2}-12xy+9x^{2}$是完全平方式的有______(填序号);
(2)若$9x^{2}+kx+16$是一个完全平方式,则$k$的值等于______($k$为常数);
(3)代数式$-2x^{2}+4x-3$有最大值还是最小值? 并求出这个最值.

答案： 14.
(1) ②④
(2) $\pm 24$
(3) 原式 $= - 2(x^2 - 2x + \frac{3}{2}) = - 2(x^2 - 2x + 1 + \frac{1}{2}) = - 2(x - 1)^2 - 1$，$\because - 2(x - 1)^2 \leq 0$，$\therefore - 2(x - 1)^2 - 1 \leq - 1$，$\therefore$ 原式有最大值 $- 1$。

15. 如图1是由边长分别为$a,b$的两个正方形拼成的图形,其面积为$S_{1}$;如图2是长、宽分别为$a,b$的长方形,其面积为$S_{2}$.

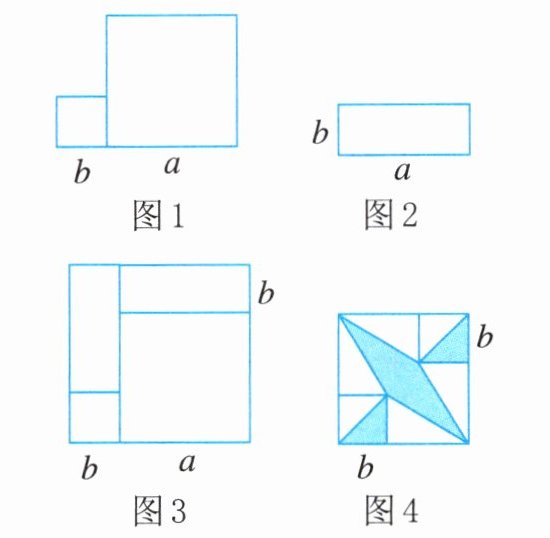
(1)如图3是由图1,2中的图形拼成的大正方形,其面积为$S_{3}$,则$S_{1},S_{2},S_{3}$的数量关系是______.
(2)在图1边长为$a的正方形中放入两个边长为b$的小正方形,得到如图4所示的图形.若$S_{1}= 13,S_{2}= 5$,求图4中阴影部分的面积.

答案： 15.
(1) $S_3 = S_1 + 2S_2$。
(2) 因为 $S_1 = 13$，$S_2 = 5$，$a ＞ b ＞ 0$，所以 $a^2 + b^2 = 13$，$ab = 5$。所以 $(a - b)^2 = a^2 + b^2 - 2ab = 3$。所以 $S_{阴影} = a^2 - b^2 - 4 × \frac{1}{2}b(a - b) = a^2 - b^2 - 2ab + 2b^2 = a^2 + b^2 - 2ab = 3$。