《2025年第三学期暑假衔接七年级数学浙教版》

1. 下列计算中正确的是()

A.$(a^{7})^{2}= a^{9}$
B.$a^{7}\cdot a^{2}= a^{14}$
C.$2a^{2}+3a^{3}= 5a^{5}$
D.$(ab)^{3}= a^{3}b^{3}$

答案： D

2. 小明想利用一个废旧的包装盒制作一个正方体小收纳箱,若该小收纳箱的棱长为$2a^{3}$,则该小收纳箱的体积为()

A.$6a^{6}$
B.$8a^{8}$
C.$8a^{9}$
D.$6a^{12}$

答案： C

3. 我国古代数学家祖冲之推算出$π的近似值为\frac {355}{113}$,它与$π$的误差小于0.0000003.将0.0000003用科学记数法可表示为()

A.$3×10^{-7}$
B.$0.3×10^{-6}$
C.$3×10^{-6}$
D.$3×10^{7}$

答案： A

4. 在数$(-\frac {1}{2})^{-2},(-2)^{-2},(\frac {1}{2})^{-1},2^{-1}$中,最小的是()

A.$(\frac {1}{2})^{-2}$
B.$(-2)^{-2}$
C.$(\frac {1}{2})^{-1}$
D.$2^{-1}$

答案： B

5. 下面计算正确的有()
①$3x^{3}(-2x^{2})= -6x^{5}$；②$3a^{2}\cdot 4a^{2}= 12a^{2}$；③$3b^{3}\cdot 8b^{3}= 24b^{9}$；④$-3x\cdot 2xy= 6x^{2}y$；⑤$-x(x^{3}-1)= -x^{4}+x$.

A.3个
B.2个
C.1个
D.0个

答案： B

6. 设$(a+3b)^{2}= (a-3b)^{2}+A$,则$A$等于()

A.$6ab$
B.$12ab$
C.$-12ab$
D.$24ab$

答案： B

7. 已知实数$a$,$b满足a-b^{2}= 4$,则代数式$a^{2}-3b^{2}+a-14$的值可以是()

A.$-5$
B.1
C.2
D.6

答案： D

8. 如图,阴影部分是边长为$a的大正方形中剪去一个边长为b$的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是()


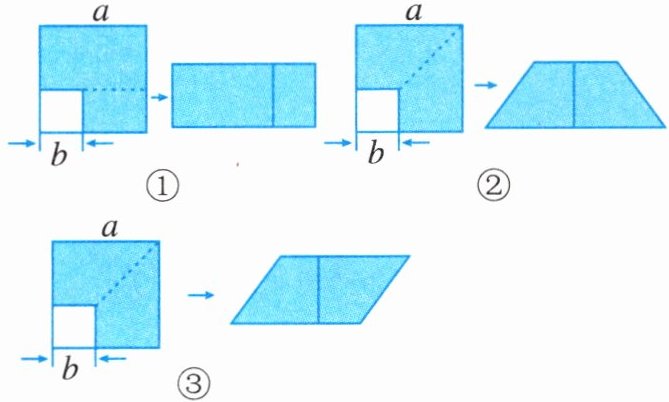
A.①②
B.②③
C.①③
D.①②③

答案： D

9. 已学的“幂的运算”有：①同底数幂的乘法；②幂的乘方；③积的乘方.在“$(a^{2}\cdot a^{3})^{2}= (a^{2})^{2}\cdot (a^{3})^{2}= a^{4}\cdot a^{6}= a^{10}$”的运算过程中,运用了上述幂的运算中的____.(按运算顺序填序号)

答案： ③②①

10. 已知$a+b= 1$,则代数式$a^{2}-b^{2}+2b+9$的值为____.

答案： 10

11. 小红计算$(x-2y)^{2}+(2x-y)(2x+y)-x(□x-3y)-2y^{2}$时,得到的结果是$x^{2}+y^{2}-xy$,则“$□$”表示的数为____.

答案： 4

12. 对于任意有理数$a$,$b$,$c$,$d$,定义一种新运算：$\begin{vmatrix} a&c\\ b&d\end{vmatrix} = a^{2}+b^{2}-cd$.则对于有理数$x$,$y$,若是一个完全平方式,则$k= $____.

答案： 8 或 -8