《2025年第三学期暑假衔接七年级数学浙教版》

12. 老师有$[(n+5)^{2}-(n-1)^{2}]$个礼物(其中$n≥1$,且n为整数).现在将这些礼物平均分给班级的同学,恰好能分完,那么下列选项中:①4;②12;③$n+2$;④$6n+8$,可以是班级的同学个数的是.

答案： ①②③

13. 某校为了解学生对“生命、生态与安全”课程的学习掌握情况,从八年级学生中随机抽取了部分学生进行综合测试. 测试结果分为 A 级、B 级、C 级、D 级四个等级,并将测试结果绘制成了如下两幅不完整的统计图. 根据统计图中的信息解答下列问题:

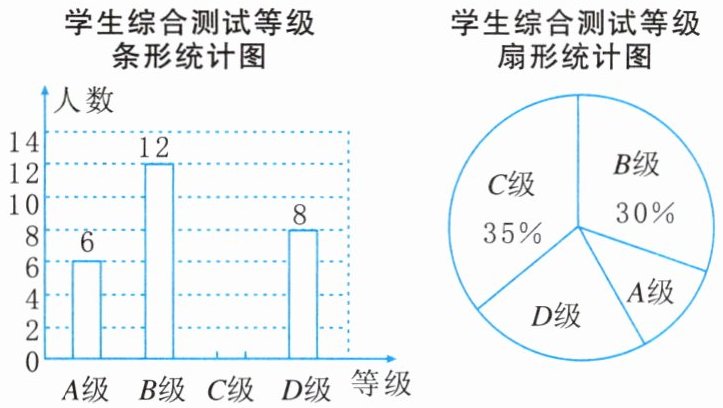
(1)本次抽样测试的学生人数是;
(2)扇形统计图中表示 D 级的扇形圆心角的度数是,并把条形统计图补充完整;
(3)该校八年级共有学生 600 人,如果全部参加这次测试,测试成绩为 A 级的学生大约有多少人?

答案：

(1) 40
(2) $72^{\circ}$ 补全的条形统计图如下.

(3) 90人

14. 如图1,将一张长方形纸片沿EF折叠,使AB落在$A'B'$的位置.
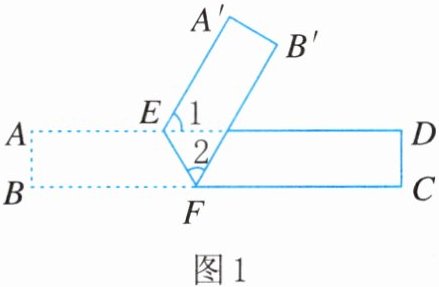
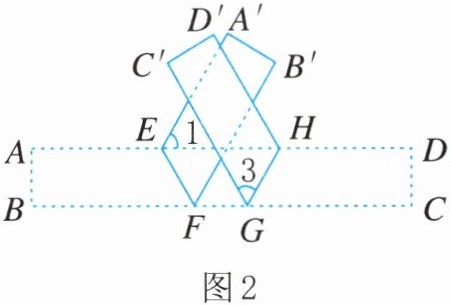
(1)若$∠1$的度数为α,试求$∠2$的度数(用含α的代数式表示);
(2)如图2,再将纸片沿GH折叠,使得CD落在$C'D'$的位置.
①若$EF// C'G,∠1$的度数为α,试求$∠3$的度数(用含α的代数式表示);
②若$B'F⊥C'G,∠3的度数比∠1的度数大20^{\circ }$,试计算$∠1$的度数.

答案：

(1) 如图，标注 $∠4$. 由题意可知， $A'E // B'F$，所以 $∠4 = ∠1 = α$. 因为 $AD // BC$，所以 $∠4 = ∠B'FC = α$. 因为 $∠BFE + ∠2 + ∠B'FC = 180^{\circ}$，又因为 $∠2 = ∠BFE$，所以 $∠2 = \frac{1}{2} × (180^{\circ} - α) = 90^{\circ} - \frac{1}{2}α$.
　　　　　　　　　　
(2) ① 由
(1) 知， $∠BFE = ∠EFB' = 90^{\circ} - \frac{1}{2}α$，因为 $EF // C'G$，所以 $∠BFE = ∠C'GB = 90^{\circ} - \frac{1}{2}α$，所以 $∠3 + ∠HGC = 180^{\circ} - (90^{\circ} - \frac{1}{2}α) = 90^{\circ} + \frac{1}{2}α$. 又因为 $∠3 = ∠HGC$，所以 $∠3 = \frac{1}{2} × (90^{\circ} + \frac{1}{2}α) = 45^{\circ} + \frac{1}{4}α$.
② 由
(1) 知， $∠BFE = ∠EFB' = 90^{\circ} - \frac{1}{2}∠1$，由 $B'F \perp C'G$ 可知， $∠B'FC + ∠FGC' = 180^{\circ} - 90^{\circ} = 90^{\circ}$，又因为 $∠FGC' = 180^{\circ} - 2∠3$，所以 $180^{\circ} - 2 × (90^{\circ} - \frac{1}{2}∠1) + (180^{\circ} - 2∠3) = 90^{\circ}$，即 $∠1 + 180^{\circ} - 2∠3 = 90^{\circ}$. 因为 $∠3 = ∠1 + 20^{\circ}$，所以 $∠1 + 180^{\circ} - 2(∠1 + 20^{\circ}) = 90^{\circ}$，解得 $∠1 = 50^{\circ}$.