2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
13. 计算:
(1)$(\frac {1}{2})^{-1}-(π-3.14)^{0}+(-1\frac {1}{2})^{2023}×(\frac {2}{3})^{2024}$;
(2)$(-2ab)(3a^{2}-2ab-b^{2})$;
(3)$(9x^{2}y-6xy^{2}+3xy)÷(3xy)$.
(1)$(\frac {1}{2})^{-1}-(π-3.14)^{0}+(-1\frac {1}{2})^{2023}×(\frac {2}{3})^{2024}$;
(2)$(-2ab)(3a^{2}-2ab-b^{2})$;
(3)$(9x^{2}y-6xy^{2}+3xy)÷(3xy)$.
答案:
(1) $\frac{1}{3}$
(2) $-6a^{3}b + 4a^{2}b^{2} + 2ab^{3}$
(3) $3x - 2y + 1$
(1) $\frac{1}{3}$
(2) $-6a^{3}b + 4a^{2}b^{2} + 2ab^{3}$
(3) $3x - 2y + 1$
14. 若两个正整数$a$,$b$,满足$(a+b)^{2}= ka+b$,$k$为自然数,则称$a为b$的“$k$级”数.例如$a= 2$,$b= 3$,$(2+3)^{2}= 11×2+3$,则2为3的“11级”数.
(1)5是6的“____级”数;正整数$n$为1的“____级”数;(用关于$n$的代数式表示)
(2)若$m$为4的“$(m+10)$级”数,求$m$的值;
(3)是否存在$a$,$b$的值,使得$a为b$的“$(a+b)$级”数?若存在,请举出一组$a$,$b$的值;若不存在,请说明理由.
(1)5是6的“____级”数;正整数$n$为1的“____级”数;(用关于$n$的代数式表示)
(2)若$m$为4的“$(m+10)$级”数,求$m$的值;
(3)是否存在$a$,$b$的值,使得$a为b$的“$(a+b)$级”数?若存在,请举出一组$a$,$b$的值;若不存在,请说明理由.
答案:
(1) 23 $(n + 2)$
(2) 6
(3) 若存在,则 $(a + b)^{2} = a(a + b) + b$,$\therefore a^{2} + 2ab + b^{2} = a^{2} + ab + b$,$\therefore b(a + b - 1) = 0$,$\because a$,$b$ 是正整数,$\therefore a \geq 1$,$b \geq 1$,$\therefore b \neq 0$,$a + b - 1 \neq 0$,$\therefore b(a + b - 1) \neq 0$,这与假设产生矛盾,$\therefore$ 不存在 $a$,$b$ 的值,使得 $a$ 为 $b$ 的“$(a + b)$ 级”数。
(1) 23 $(n + 2)$
(2) 6
(3) 若存在,则 $(a + b)^{2} = a(a + b) + b$,$\therefore a^{2} + 2ab + b^{2} = a^{2} + ab + b$,$\therefore b(a + b - 1) = 0$,$\because a$,$b$ 是正整数,$\therefore a \geq 1$,$b \geq 1$,$\therefore b \neq 0$,$a + b - 1 \neq 0$,$\therefore b(a + b - 1) \neq 0$,这与假设产生矛盾,$\therefore$ 不存在 $a$,$b$ 的值,使得 $a$ 为 $b$ 的“$(a + b)$ 级”数。
15. 有两个正方形$A$,$B$,现将$B放在A$的内部得图甲,将$A$,$B$并列放置后构造新的正方形得图乙。图甲和图乙中阴影部分的面积分别为1和12.
(1)正方形$A$,$B$的面积之和为____;
(2)若三个正方形$A和两个正方形B$如图丙摆放,求阴影部分的面积.
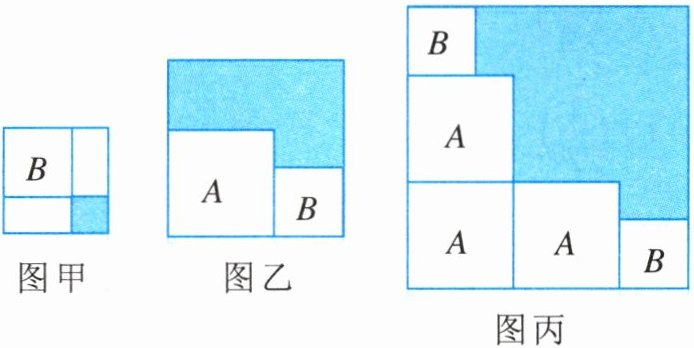
(1)正方形$A$,$B$的面积之和为____;
(2)若三个正方形$A和两个正方形B$如图丙摆放,求阴影部分的面积.

答案:
(1) 13
(2) $\because ab = 6$,$a^{2} + b^{2} = 13$,$\therefore (a + b)^{2} = (a - b)^{2} + 4ab = 1 + 24 = 25$,$\because a + b > 0$,$\therefore a + b = 5$,$\because (a - b)^{2} = 1$,且 $a > b$,$\therefore a - b = 1$,$\therefore$ 图丙的阴影部分面积 $S = (2a + b)^{2} - 3a^{2} - 2b^{2} = a^{2} - b^{2} + 4ab = (a - b)(a + b) + 4ab = 5 + 24 = 29$。
(1) 13
(2) $\because ab = 6$,$a^{2} + b^{2} = 13$,$\therefore (a + b)^{2} = (a - b)^{2} + 4ab = 1 + 24 = 25$,$\because a + b > 0$,$\therefore a + b = 5$,$\because (a - b)^{2} = 1$,且 $a > b$,$\therefore a - b = 1$,$\therefore$ 图丙的阴影部分面积 $S = (2a + b)^{2} - 3a^{2} - 2b^{2} = a^{2} - b^{2} + 4ab = (a - b)(a + b) + 4ab = 5 + 24 = 29$。
查看更多完整答案,请扫码查看


