《2025年第三学期暑假衔接七年级数学浙教版》

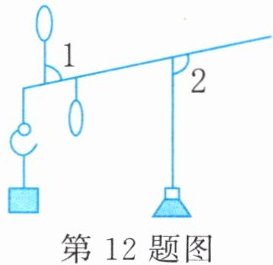
12. 一杆古秤在称物体时的状态如图所示,已知 $ \angle 2 = 100^{\circ} $,则 $ \angle 1 $ 的度数是 ______.

答案： $80^{\circ}$

13. 如图,已知 $ AB // CD // PN $,$ \angle ABC = 50^{\circ} $,$ \angle CPN = 150^{\circ} $,求 $ \angle BCP $ 的度数.

答案： $20^{\circ}$

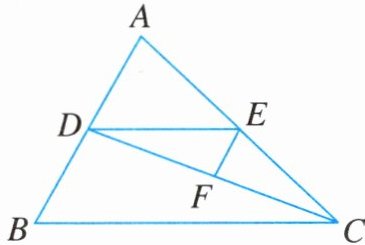
14. 如图,已知 $ \angle CFE + \angle BDC = 180^{\circ} $,$ \angle DEF = \angle B $. 试判断 $ \angle AED $ 与 $ \angle ACB $ 的大小关系,并说明理由.

答案：
$\angle AED=\angle ACB$。理由：如图

$\because\angle 1+\angle 4=180^{\circ},\angle 1+\angle 2=180^{\circ},\therefore\angle 2=\angle 4.\therefore EF// AB$。
$\therefore\angle 3=\angle ADE.\because\angle 3=\angle B$，
$\therefore\angle B=\angle ADE.\therefore DE// BC.\therefore\angle AED=\angle ACB$。

15. 已知直线 $ AB // CD $,点 $ E $,$ F $ 分别在直线 $ AB $,$ CD $ 上,$ \angle EFD = \alpha $. 点 $ P $ 是直线 $ AB $ 上的动点(不与 $ E $ 重合),连结 $ PF $,$ \angle PEF $ 和 $ \angle PFC $ 的平分线所在直线交于点 $ H $.

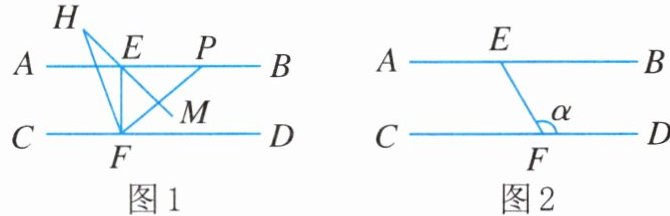
(1)如图 1,若 $ EF \perp CD $,点 $ P $ 在射线 $ EB $ 上. 则当 $ \angle EPF = 40^{\circ} $ 时,$ \angle EHF = $ ______；
(2)如图 2,若 $ \alpha = 120^{\circ} $,点 $ P $ 在射线 $ EA $ 上.
① 补全图形；
② 探究 $ \angle EPF $ 与 $ \angle EHF $ 的数量关系,并证明你的结论.

答案：

(1)$25^{\circ}$
(2)①若$\alpha =120^{\circ}$，点$P$在射线$EA$上，补全图形，如图所示。
②$\angle EPF$与$\angle EHF$的数量关系是$\angle EHF=\frac{1}{2}\angle EPF + 60^{\circ}$，证明如下：
$\because AB// CD,\therefore\angle PEF=\angle EFD=\alpha =120^{\circ},\angle EPF=\angle PFC.$
$\because EM,FH$分别平分$\angle PEF,\angle PFC,\therefore\angle FEM=\frac{1}{2}\angle PEF=60^{\circ}$，
$\angle CFH=\frac{1}{2}\angle PFC,\therefore\angle CFH=\frac{1}{2}\angle EPF.$
$\because\angle EFM=180^{\circ}-\alpha =60^{\circ},\therefore\angle FMH=180^{\circ}-\angle FEM-\angle EFM=60^{\circ}.$
$\because\angle EHF=\angle CFH+\angle FMH,\therefore\angle EHF=\frac{1}{2}\angle EPF+60^{\circ}$。