2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12. 已知$\angle ABG$为锐角,$AH// BG$,点$C从点B$(点$C不与点B$重合)出发,沿射线$BG$的方向移动,$CD// AB交直线AH于点D$,$CE\perp CD交AB于点E$,$CF\perp AD$,垂足为点$F$(点$F不与点A$重合).若$\angle ECF= n^{\circ}$,则$\angle BAF= $______.(用含$n$的代数式表示)
答案:
n°或180° - n°
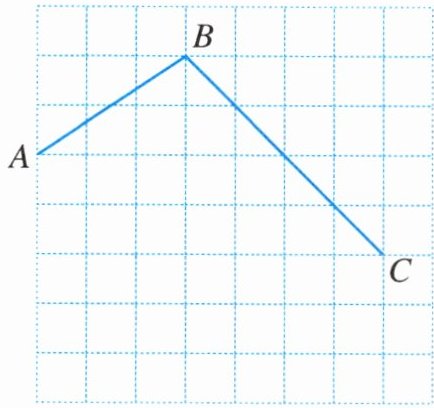
13. 如图,在方格纸中,有两条线段$AB$,$BC$.利用方格纸完成以下操作:
(1)过点$A作BC$的平行线;
(2)过点$C作AB$的平行线,与(1)中的平行线相交于点$D$;
(3)过点$B作BC的垂线l$;
(4)用符号表示出图中的一组平行线______.
(1)过点$A作BC$的平行线;
(2)过点$C作AB$的平行线,与(1)中的平行线相交于点$D$;
(3)过点$B作BC的垂线l$;
(4)用符号表示出图中的一组平行线______.

答案:
(1)如图,AD即为所求。
(2)如图,CD即为所求。
(3)如图,l即为所求。
(4)AD//BC(或AB//DC)。

(1)如图,AD即为所求。
(2)如图,CD即为所求。
(3)如图,l即为所求。
(4)AD//BC(或AB//DC)。

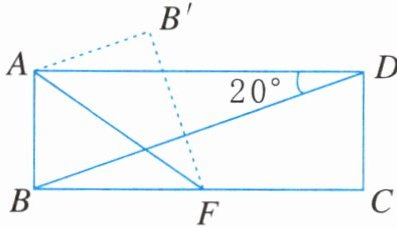
14. 如图,把一张长方形纸片$ABCD沿AF$折叠,使$B点落在点B'$处,折叠后展开满足$AB'// BD$,$\angle ADB= 20^{\circ}$,求$\angle BAF$的度数.

答案:
55°
15. 某学习小组发现一个结论:已知直线$a// b$,若直线$c// a$,则$c// b$.他们发现这个结论应用很广,请你利用这个结论解决以下问题:
已知直线$AB// CD$,点$E在AB$,$CD$之间,点$P$,$Q分别在直线AB$,$CD$上,连结$PE$,$EQ$.
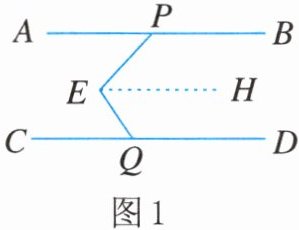
(1)如图1,过点$E作EH// AB$,运用上述结论,探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系,并说明理由;
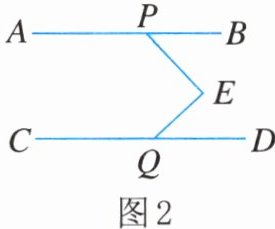
(2)如图2,类比(1)中的方法,运用上述结论,探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系,并说明理由;
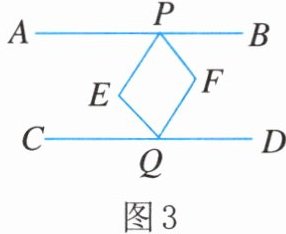
(3)如图3,$PF平分\angle BPE$,$QF平分\angle EQD$,当$PEQ= 140^{\circ}$时,请直接写出$\angle PFQ$的度数.
已知直线$AB// CD$,点$E在AB$,$CD$之间,点$P$,$Q分别在直线AB$,$CD$上,连结$PE$,$EQ$.
(1)如图1,过点$E作EH// AB$,运用上述结论,探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系,并说明理由;
(2)如图2,类比(1)中的方法,运用上述结论,探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系,并说明理由;
(3)如图3,$PF平分\angle BPE$,$QF平分\angle EQD$,当$PEQ= 140^{\circ}$时,请直接写出$\angle PFQ$的度数.



答案:
$(1)$探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系
解:$\angle PEQ=\angle APE+\angle CQE$。
理由如下:
因为$EH// AB$,$AB// CD$,根据“已知直线$a// b$,若直线$c// a$,则$c// b$”,所以$EH// CD$。
根据两直线平行,内错角相等,可得$\angle APE = \angle PEH$,$\angle CQE=\angle QEH$。
又因为$\angle PEQ=\angle PEH+\angle QEH$,所以$\angle PEQ=\angle APE+\angle CQE$。
$(2)$探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系
解:$\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)$。
理由如下:
过点$E$作$EF// AB$,因为$AB// CD$,所以$EF// CD$。
根据两直线平行,同旁内角互补,可得$\angle APE+\angle PEF = 180^{\circ}$,$\angle CQE+\angle QEF = 180^{\circ}$。
所以$\angle APE+\angle PEF+\angle CQE+\angle QEF=180^{\circ}+180^{\circ}=360^{\circ}$,即$\angle APE+\angle CQE+\angle PEQ = 360^{\circ}$,所以$\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)$。
$(3)$求$\angle PFQ$的度数
解:
由$(2)$可知$\angle BPE+\angle EQD=360^{\circ}-\angle PEQ$,因为$\angle PEQ = 140^{\circ}$,所以$\angle BPE+\angle EQD=360^{\circ}- 140^{\circ}=220^{\circ}$。
因为$PF$平分$\angle BPE$,$QF$平分$\angle EQD$,所以$\angle FPE=\frac{1}{2}\angle BPE$,$\angle FQD=\frac{1}{2}\angle EQD$。
过点$F$作$FG// AB$,因为$AB// CD$,所以$FG// CD$。
根据两直线平行,内错角相等,可得$\angle PFG=\angle FPE$,$\angle QFG=\angle FQD$。
所以$\angle PFQ=\angle PFG+\angle QFG=\frac{1}{2}(\angle BPE+\angle EQD)=\frac{1}{2}×220^{\circ}=110^{\circ}$。
综上,答案依次为:$(1)$$\boldsymbol{\angle PEQ=\angle APE+\angle CQE}$;$(2)$$\boldsymbol{\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)}$;$(3)$$\boldsymbol{110^{\circ}}$。
解:$\angle PEQ=\angle APE+\angle CQE$。
理由如下:
因为$EH// AB$,$AB// CD$,根据“已知直线$a// b$,若直线$c// a$,则$c// b$”,所以$EH// CD$。
根据两直线平行,内错角相等,可得$\angle APE = \angle PEH$,$\angle CQE=\angle QEH$。
又因为$\angle PEQ=\angle PEH+\angle QEH$,所以$\angle PEQ=\angle APE+\angle CQE$。
$(2)$探究$\angle PEQ$,$\angle APE$,$\angle CQE$之间的数量关系
解:$\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)$。
理由如下:
过点$E$作$EF// AB$,因为$AB// CD$,所以$EF// CD$。
根据两直线平行,同旁内角互补,可得$\angle APE+\angle PEF = 180^{\circ}$,$\angle CQE+\angle QEF = 180^{\circ}$。
所以$\angle APE+\angle PEF+\angle CQE+\angle QEF=180^{\circ}+180^{\circ}=360^{\circ}$,即$\angle APE+\angle CQE+\angle PEQ = 360^{\circ}$,所以$\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)$。
$(3)$求$\angle PFQ$的度数
解:
由$(2)$可知$\angle BPE+\angle EQD=360^{\circ}-\angle PEQ$,因为$\angle PEQ = 140^{\circ}$,所以$\angle BPE+\angle EQD=360^{\circ}- 140^{\circ}=220^{\circ}$。
因为$PF$平分$\angle BPE$,$QF$平分$\angle EQD$,所以$\angle FPE=\frac{1}{2}\angle BPE$,$\angle FQD=\frac{1}{2}\angle EQD$。
过点$F$作$FG// AB$,因为$AB// CD$,所以$FG// CD$。
根据两直线平行,内错角相等,可得$\angle PFG=\angle FPE$,$\angle QFG=\angle FQD$。
所以$\angle PFQ=\angle PFG+\angle QFG=\frac{1}{2}(\angle BPE+\angle EQD)=\frac{1}{2}×220^{\circ}=110^{\circ}$。
综上,答案依次为:$(1)$$\boldsymbol{\angle PEQ=\angle APE+\angle CQE}$;$(2)$$\boldsymbol{\angle PEQ = 360^{\circ}-(\angle APE+\angle CQE)}$;$(3)$$\boldsymbol{110^{\circ}}$。
查看更多完整答案,请扫码查看


