《2025年第三学期暑假衔接七年级数学浙教版》

13. 为提升城市形象,缓解交通拥堵状况,某市积极实施城市快速路整修工程. 现有甲、乙两个工程队参与整修. 已知甲工程队单独整修 600 米道路与乙工程队单独整修 750 米道路所用天数相同,乙队每天比甲队多整修 30 米.
(1)甲、乙两队每天各整修道路多少米?
(2)这段快速路全长 3000 米,现由甲、乙两工程队从两端同时整修,各用了正整数天完成了任务,且甲工程队修路的天数不足 15 天,问甲、乙两工程队各修了多少天?

答案：
(1) 设甲工程队每天整修道路 $x$ 米，则乙工程队每天整修道路 $(x + 30)$ 米，根据题意得： $ \frac{600}{x} = \frac{750}{x + 30} $，解得 $x = 120$，经检验， $x = 120$ 是原方程的解. 且符合题意. $ \therefore x + 30 = 120 + 30 = 150$. 答：甲工程队每天整修道路 120 米，乙工程队每天整修道路 150 米.
(2) 设甲工程队整修了 $m$ 天，乙工程队整修了 $n$ 天，根据题意得： $120m + 150n = 3000$， $ \therefore n = 20 - \frac{4}{5}m$，又 $ \because m$， $n$ 均为正整数，且 $m ＜ 15$， $ \therefore \begin{cases} m = 5, \\ n = 16 \end{cases} $ 或 $ \begin{cases} m = 10, \\ n = 12. \end{cases} $ 答：甲、乙两工程队分别修了 5 天、16 天或 10 天、12 天.

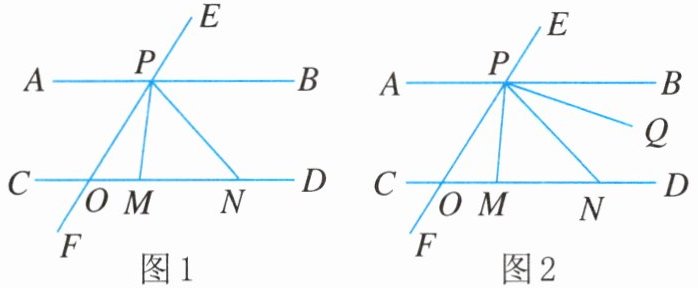
14. 已知直线$AB// CD$,经过直线 AB 上的定点 P 的直线 EF 交 CD 于点 O,M,N 为直线 CD 上的两点,且点 M 在点 O 右侧,点 N 的左侧时,连结 PM,PN,满足$∠MPN= ∠MNP.$
(1)如图1,若$∠MPO= 25^{\circ },∠MNP= 50^{\circ }$,则$∠COP= $;
(2)如图2,射线 PQ 为$∠MPE$的平分线,用等式表示$∠NPQ与∠POM$之间的数量关系,并说明理由.

答案：
(1) $125^{\circ}$
(2) $∠POM = 2∠NPQ$. 理由：因为 $AB // CD$，所以 $∠EPB = ∠POD$， $∠BPN = ∠PNM$. 又因为射线 $PQ$ 为 $∠MPE$ 的平分线，所以 $∠EPQ = ∠MPQ = \frac{1}{2}∠MPE$. 因为 $∠MPN = ∠PNM = ∠NPB$，所以 $∠MPN = ∠NPB = \frac{1}{2}(∠MPN + ∠NPB) = \frac{1}{2}∠MPB$，所以 $∠NPQ = ∠MPQ - ∠MPN = \frac{1}{2}∠MPE - \frac{1}{2}∠MPB = \frac{1}{2}∠EPB = \frac{1}{2}∠POM$，即 $∠POM = 2∠NPQ$.

15. 已知用$[a]$表示不大于a的最大整数,如$[3.2]= 3,[-4.2]= -5.$
(1)求$[3.2]+[-1.8]$的值;
(2)若x,y满足$\left\{\begin{array}{l} [x]-[y]= -3,\\ 2[x]+[y]= 15,\end{array} \right. 求[x]+[y]$的值;
(3)已知$\frac {1}{2}[x]+[y]= m,[x-\frac {3}{2}]+2[y]= n.$
①写出$2m-n$的所有可能值;
②若$m+n= 14$,请直接写出一对符合条件的x,y的解:$\left\{\begin{array}{l} x= ,\\ y= \end{array} \right. $

答案：
(1) $ [3.2] + [-1.8] = 3 + (-2) = 3 - 2 = 1 $.
(2) $ \begin{cases} [x] - [y] = -3, ① \\ 2[x] + [y] = 15, ② \end{cases} $ ① + ② 得 $ 3[x] = 12 $，解得 $ [x] = 4 $. 把 $ [x] = 4 $ 代入 ① 得， $ 4 - [y] = -3 $，解得 $ [y] = 7 $， $ \therefore [x] + [y] = 4 + 7 = 11 $.
(3) ① $ \because \frac{1}{2}[x] + [y] = m $， $ [x - \frac{3}{2}] + 2[y] = n $， $ \therefore 2m - n = [x] + 2[y] - [x - \frac{3}{2}] - 2[y] = [x] - [x - \frac{3}{2}] $. 设 $x$ 的小数部分为 $t$，当 $0 ＜ t ＜ 0.5$ 时， $ [x] = x - t $， $ [x - \frac{3}{2}] = x - 2 - t $， $ \therefore [x] - [x - \frac{3}{2}] = x - t - (x - 2 - t) = 2 $；当 $0.5 \leq t ＜ 1$ 时， $ [x] = x - t $， $ [x - \frac{3}{2}] = x - 1 - t $， $ \therefore [x] - [x - \frac{3}{2}] = x - t - (x - 1 - t) = 1 $. 综上所述， $ 2m - n = 1 $ 或 $ 2m - n = 2 $.
② 2.6 4