2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 关于 $ x,y $ 的二元一次方程组 $ \begin{cases} y = x + 4, \\ 3x + y = 8, \end{cases} $ 用代入法消去 $ y $ 后所得到的方程正确的是()
A.$ 3x - x - 4 = 8 $
B.$ 3x + x - 4 = 8 $
C.$ 3x + x + 4 = 8 $
D.$ 3x - x + 4 = 8 $
A.$ 3x - x - 4 = 8 $
B.$ 3x + x - 4 = 8 $
C.$ 3x + x + 4 = 8 $
D.$ 3x - x + 4 = 8 $
答案:
C
2. 用加减消元法解二元一次方程组 $ \begin{cases} x + 3y = 4,① \\ 2x - y = 1② \end{cases} $ 时,下列方法中,无法消元的是()
A.$ ①×2 - ② $
B.$ ②×(-3) - ① $
C.$ ①×(-2) + ② $
D.$ ① - ②×3 $
A.$ ①×2 - ② $
B.$ ②×(-3) - ① $
C.$ ①×(-2) + ② $
D.$ ① - ②×3 $
答案:
D
3. 下列用代入法解方程组 $ \begin{cases} 2x + 3y = 8,① \\ 3x - 5y = 5② \end{cases} $ 的过程中,开始出现错误的一步是()
Ⅰ. 由①,得 $ x = \frac{8 - 3y}{2} $. ③
Ⅱ. 把③代入②,得 $ 3×\frac{8 - 3y}{2} - 5y = 5 $.
Ⅲ. 去分母,得 $ 24 - 9y - 10y = 5 $.
Ⅳ. 解得 $ y = 1 $,再代入③,得 $ x = 2.5 $.
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
Ⅰ. 由①,得 $ x = \frac{8 - 3y}{2} $. ③
Ⅱ. 把③代入②,得 $ 3×\frac{8 - 3y}{2} - 5y = 5 $.
Ⅲ. 去分母,得 $ 24 - 9y - 10y = 5 $.
Ⅳ. 解得 $ y = 1 $,再代入③,得 $ x = 2.5 $.
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
答案:
C
4. 在解二元一次方程组 $ \begin{cases} 6x + \bigoplus y = 9,① \\ 2x + \bigotimes y = -6② \end{cases} $ 时,若① - ②可直接消去未知数 $ y $,则 $ \bigoplus $ 和 $ \bigotimes $()
A.互为倒数
B.大小相等
C.都等于 0
D.互为相反数
A.互为倒数
B.大小相等
C.都等于 0
D.互为相反数
答案:
B
5. 用加减消元法将方程组 $ \begin{cases} 2x - 3y = 9, \\ 2x + 4y = -1 \end{cases} $ 中的 $ x $ 消去后得到的方程是()
A.$ y = 8 $
B.$ 7y = 10 $
C.$ -7y = 8 $
D.$ -7y = 10 $
A.$ y = 8 $
B.$ 7y = 10 $
C.$ -7y = 8 $
D.$ -7y = 10 $
答案:
D
6. 用加减消元法解方程组 $ \begin{cases} 2x + 3y = 1, \\ 3x - 2y = 8 \end{cases} $ 时,有以下四种变形,其中变形正确的是()
① $ \begin{cases} 6x + 9y = 1, \\ 6x - 4y = 8; \end{cases} $
② $ \begin{cases} 4x + 6y = 1, \\ 9x - 6y = 8; \end{cases} $
③ $ \begin{cases} 6x + 9y = 3, \\ 6x - 4y = 16; \end{cases} $
④ $ \begin{cases} 4x + 6y = 2, \\ 9x - 6y = 24. \end{cases} $
A.①②
B.③④
C.①③
D.②④
① $ \begin{cases} 6x + 9y = 1, \\ 6x - 4y = 8; \end{cases} $
② $ \begin{cases} 4x + 6y = 1, \\ 9x - 6y = 8; \end{cases} $
③ $ \begin{cases} 6x + 9y = 3, \\ 6x - 4y = 16; \end{cases} $
④ $ \begin{cases} 4x + 6y = 2, \\ 9x - 6y = 24. \end{cases} $
A.①②
B.③④
C.①③
D.②④
答案:
B
7. 已知方程组 $ \begin{cases} 3x + 5y = 3k + 1, \\ 5x + 3y = k + 1, \end{cases} $ $ x $ 与 $ y $ 的值之和等于 2,则 $ k $ 的值为()
A.$ -2 $
B.$ -\frac{7}{2} $
C.2
D.$ \frac{7}{2} $
A.$ -2 $
B.$ -\frac{7}{2} $
C.2
D.$ \frac{7}{2} $
答案:
D
8. 小亮解方程组 $ \begin{cases} 2x + y = ●, \\ 2x - y = 12 \end{cases} $ 得  由于不小心,滴上了两滴墨水,刚好遮住了两个数 ● 和 ★,请你帮他计算,● = ______,★ = ______.()
由于不小心,滴上了两滴墨水,刚好遮住了两个数 ● 和 ★,请你帮他计算,● = ______,★ = ______.()
A.8,-2
B.-8,2
C.6,-4
D.4,-6
 由于不小心,滴上了两滴墨水,刚好遮住了两个数 ● 和 ★,请你帮他计算,● = ______,★ = ______.()
由于不小心,滴上了两滴墨水,刚好遮住了两个数 ● 和 ★,请你帮他计算,● = ______,★ = ______.()A.8,-2
B.-8,2
C.6,-4
D.4,-6
答案:
A
9. 已知 $ \begin{cases} x = 3 - t, \\ y + 1 = t, \end{cases} $ 用含 $ x $ 的代数式表示 $ y $,$ y = $______.
答案:
$-x + 2$
10. 若方程组 $ \begin{cases} 3x + 4y = 9, \\ 2x + 5y = 13 \end{cases} $ 的解为  则方程组
则方程组  的解为
的解为 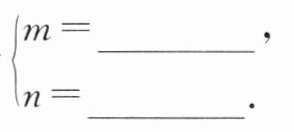
 则方程组
则方程组  的解为
的解为 
答案:
4 0
11. 已知关于 $ x,y $ 的二元一次方程组 $ \begin{cases} ax - y = 4, \\ 3x + by = 4 \end{cases} $ 的解是  则 $ a + b $ 的值是______.
则 $ a + b $ 的值是______.
 则 $ a + b $ 的值是______.
则 $ a + b $ 的值是______.
答案:
2
查看更多完整答案,请扫码查看


