2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
13. 计算:
(1)$(-2m^{2}n^{2})^{2}÷(\frac {1}{2}m^{2}n)\cdot (-2mn)$;
(2)$(x+y)^{2}-(x-y)(x+y)$.
(1)$(-2m^{2}n^{2})^{2}÷(\frac {1}{2}m^{2}n)\cdot (-2mn)$;
(2)$(x+y)^{2}-(x-y)(x+y)$.
答案:
(1)$-16m^{3}n^{4}$
(2)$2y^{2}+2xy$
(1)$-16m^{3}n^{4}$
(2)$2y^{2}+2xy$
14. 规定两数a,b之间的一种新运算※,如果$a^{c}= b$,那么$a※b= c$.
例如:因为$5^{2}= 25$,所以$5※25= 2$.因为$5^{0}= 1$.所以$5※1= 0$.
(1)根据上述规定,填空:$2※8= $______,$2※\frac {1}{16}= $______;
(2)在运算时,按以上规定:设$4※5= x$,$4※6= y$,请你说明下面这个等式成立:$4※5+4※6= 4※30$.
例如:因为$5^{2}= 25$,所以$5※25= 2$.因为$5^{0}= 1$.所以$5※1= 0$.
(1)根据上述规定,填空:$2※8= $______,$2※\frac {1}{16}= $______;
(2)在运算时,按以上规定:设$4※5= x$,$4※6= y$,请你说明下面这个等式成立:$4※5+4※6= 4※30$.
答案:
(1)3 - 4
(2)
∵$4※5 = x$,$4※6 = y$,
∴$4^{x}=5$,$4^{y}=6$。
∴$4^{x}×4^{y}=4^{x + y}=5×6 = 30$。
∴右边 = $4※30 = x + y$,左边 = x + y,
∴左边 = 右边,即$4※5 + 4※6 = 4※30$成立。
(1)3 - 4
(2)
∵$4※5 = x$,$4※6 = y$,
∴$4^{x}=5$,$4^{y}=6$。
∴$4^{x}×4^{y}=4^{x + y}=5×6 = 30$。
∴右边 = $4※30 = x + y$,左边 = x + y,
∴左边 = 右边,即$4※5 + 4※6 = 4※30$成立。
15. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了$(a+b)^{n}$(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应$(a+b)^{2}= a^{2}+2ab+b^{2}$展开式中的系数;第四行的四个数1,3,3,1,恰好对应$(a+b)^{3}= a^{3}+3a^{2}b+3ab^{2}+b^{3}$展开式中的系数.
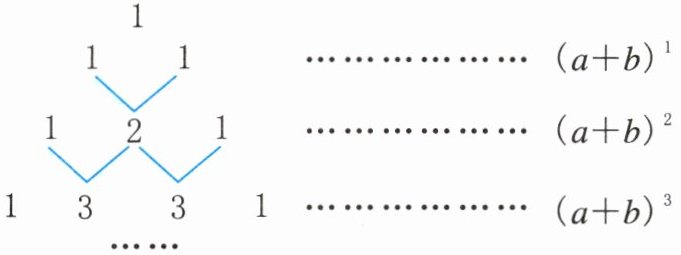
(1)根据上面的规律,写出$(a+b)^{5}$的展开式;
(2)利用上面的规律计算:$2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2-1$.
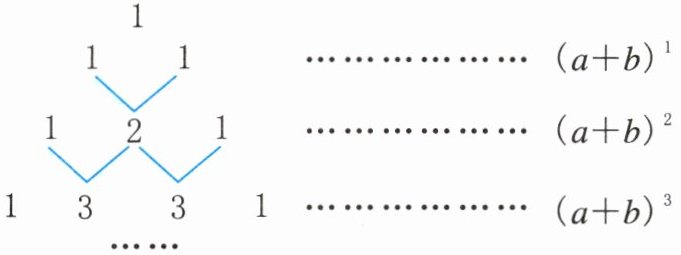
(1)根据上面的规律,写出$(a+b)^{5}$的展开式;
(2)利用上面的规律计算:$2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2-1$.
答案:
(1)$(a + b)^{5}=a^{5}+5a^{4}b + 10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$。
(2)原式 = $2^{5}+5×2^{4}×(-1)+10×2^{3}×(-1)^{2}+10×2^{2}×(-1)^{3}+5×2×(-1)^{4}+(-1)^{5}=(2 - 1)^{5}=1$。
(1)$(a + b)^{5}=a^{5}+5a^{4}b + 10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$。
(2)原式 = $2^{5}+5×2^{4}×(-1)+10×2^{3}×(-1)^{2}+10×2^{2}×(-1)^{3}+5×2×(-1)^{4}+(-1)^{5}=(2 - 1)^{5}=1$。
查看更多完整答案,请扫码查看


