2025年第三学期暑假衔接七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年第三学期暑假衔接七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 如图1,将长方形纸带沿$EF$折叠,$\angle AEF= 70^{\circ}$,再沿$GH$折叠成图2,则图2中$\angle EHB'= $______.
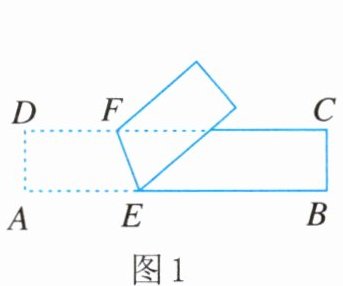
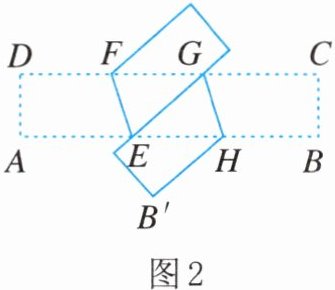


答案:
40°
12. 图1是一盏台灯,图2是其侧面示意图,已知$AB// FE$,$\angle D= 140^{\circ}$,$\angle DCB= 77^{\circ}$,则$\angle E= $______$^{\circ}$.


答案:
117
13. 如图所示,在每个小正方形的边长为1的网格中,平移三角形$ABC$,并将三角形$ABC的一个顶点A平移到D$处.
(1)请你作出平移后的三角形$DEF$;
(2)请求出三角形$DEF$的面积.
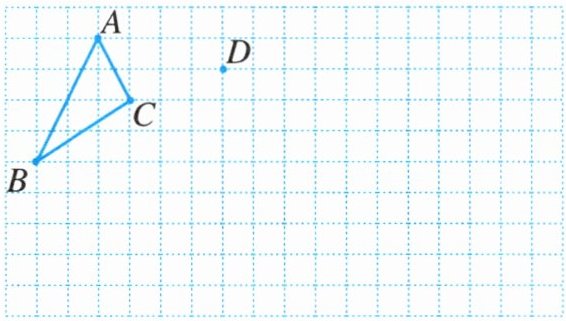
(1)请你作出平移后的三角形$DEF$;
(2)请求出三角形$DEF$的面积.
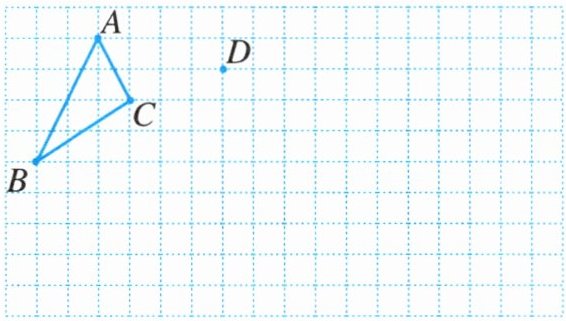
答案:
(1)如图所示,△DEF即为所求.

(2)S△DEF = 3×4 - $\frac{1}{2}$×2×4 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3 = 4
(1)如图所示,△DEF即为所求.

(2)S△DEF = 3×4 - $\frac{1}{2}$×2×4 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3 = 4
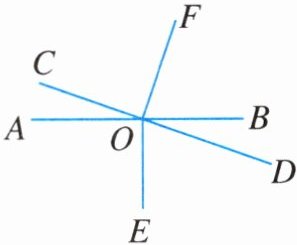
14. 如图,直线$AB$,$CD相交于点O$,$OE\perp AB$.
(1)若$\angle BOF= \angle DOE$,试说明$OF\perp CD$的理由;
(2)在(1)的条件下,若$\angle BOC-\angle AOF= \angle AOC$,求$\angle COE$的度数.
(1)若$\angle BOF= \angle DOE$,试说明$OF\perp CD$的理由;
(2)在(1)的条件下,若$\angle BOC-\angle AOF= \angle AOC$,求$\angle COE$的度数.

答案:
(1)因为OE⊥AB,所以∠BOE = ∠AOE = 90°。所以∠DOE + ∠BOD = 90°。因为∠BOF = ∠DOE,所以∠BOF + ∠BOD = 90°,所以∠DOF = 90°。所以OF⊥CD。
(2)120°
(1)因为OE⊥AB,所以∠BOE = ∠AOE = 90°。所以∠DOE + ∠BOD = 90°。因为∠BOF = ∠DOE,所以∠BOF + ∠BOD = 90°,所以∠DOF = 90°。所以OF⊥CD。
(2)120°
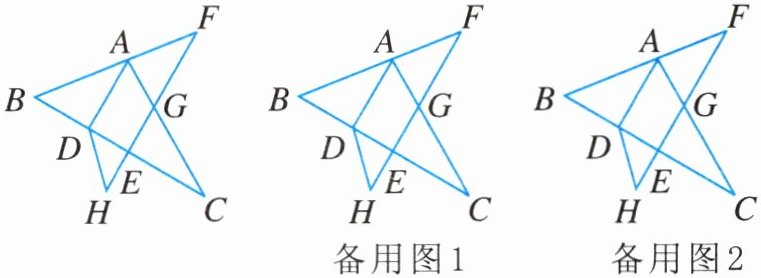
15. 如图,$AD交BC于点D$,点$F在BA$的延长线上,点$E在线段CD$上,$EF与AC相交于点G$,$\angle BDA+\angle CEG= 180^{\circ}$.
(1)证明:$AD// EF$;
(2)若点$H在FE$的延长线上,且$\angle EDH= \angle C$,$\angle F= \angle H$,则$\angle BAD和\angle CAD$相等吗?请说明理由;
(3)在(2)的条件下,若$FH\perp BC$,$\angle C= 30^{\circ}$,求$\angle F$的度数.
(1)证明:$AD// EF$;
(2)若点$H在FE$的延长线上,且$\angle EDH= \angle C$,$\angle F= \angle H$,则$\angle BAD和\angle CAD$相等吗?请说明理由;
(3)在(2)的条件下,若$FH\perp BC$,$\angle C= 30^{\circ}$,求$\angle F$的度数.

答案:
(1)
∵∠BDA + ∠CEG = 180°,∠BDA + ∠ADC = 180°,
∴∠ADC = ∠CEG。
∴AD//EF。
(2)∠BAD和∠CAD相等,理由如下:
∵∠EDH = ∠C,
∴DH//AC。
∴∠H = ∠CGH。
∵∠CGH = ∠AGF,
∴∠H = ∠AGF。
∵∠F = ∠H,
∴∠F = ∠AGF。
∵AD//EF,
∴∠BAD = ∠F,∠CAD = ∠AGF,
∴∠BAD = ∠CAD。
(3)60°
(1)
∵∠BDA + ∠CEG = 180°,∠BDA + ∠ADC = 180°,
∴∠ADC = ∠CEG。
∴AD//EF。
(2)∠BAD和∠CAD相等,理由如下:
∵∠EDH = ∠C,
∴DH//AC。
∴∠H = ∠CGH。
∵∠CGH = ∠AGF,
∴∠H = ∠AGF。
∵∠F = ∠H,
∴∠F = ∠AGF。
∵AD//EF,
∴∠BAD = ∠F,∠CAD = ∠AGF,
∴∠BAD = ∠CAD。
(3)60°
查看更多完整答案,请扫码查看


