《2025年春如金卷课时作业AB本九年级数学上册北师大版》

4. 给$□ ABCD$添加下列条件后，仍不能使它成为矩形的是（D）
A. $AB\perp BC$
B. $AC=BD$
C. $\angle A=\angle B$
D. $BC=CD$

答案： D

5. 工人师傅在制作门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形。请根据所学知识，写出其中应用的矩形的判定定理：对角线相等的平行四边形是矩形。

答案： 对角线相等的平行四边形是矩形

6. 如图，在$□ ABCD$中，$BE$平分$\angle ABC$，且与$AD$边交于点$E$，$\angle AEB=45^{\circ}$，求证：四边形$ABCD$是矩形。
证明：$\because$四边形$ABCD$为平行四边形，
$\therefore$$AD// BC$，
$\therefore$$\angle AEB=\angle EBC$。
$\because BE$平分$\angle ABC,\angle AEB=45^{\circ}$，
$\therefore$$\angle ABE=\angle EBC=45^{\circ}$，
$\therefore$$\angle ABC=90^{\circ}$，
$\therefore □ ABCD$是矩形。

答案： 证明：$\because$四边形$ABCD$为平行四边形，
$\therefore AD// BC$，
$\therefore \angle AEB=\angle EBC$。
$\because BE$平分$\angle ABC,\angle AEB=45^{\circ}$，
$\therefore \angle ABE=\angle EBC=45^{\circ}$，
$\therefore \angle ABC=90^{\circ}$，
$\therefore \square ABCD$是矩形。

7. 如图，在$□ ABCD$中，对角线$AC$，$BD$相交于点$O$，且$OA=OB$。求证：四边形$ABCD$是矩形。
证明：$\because$在平行四边形$ABCD$中，$OB=OD,OA=OC$，又$\because OA=OB$，$\therefore BD=AC$，$\therefore$平行四边形$ABCD$是矩形。

答案： 证明：$\because$在平行四边形$ABCD$中，$OB=OD,OA=OC$，
又$\because OA=OB$，
$\therefore BD=AC$，
$\therefore$平行四边形$ABCD$是矩形。

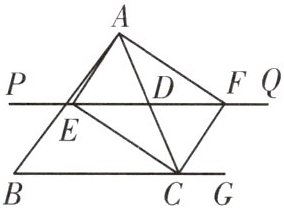
8. 如图，在$\triangle ABC$中，点$D$是$AC$边的中点，过点$D$作直线$PQ// BC$，作$\angle BCA$的平分线交直线$PQ$于点$E$，点$G$是$\triangle ABC$的边$BC$延长线上一点，作$\angle ACG$的平分线交直线$PQ$于点$F$，连接$AE$，$AF$。求证：四边形$AECF$是矩形。

答案： 证明：$\because PQ// BC$，
$\therefore \angle DEC=\angle BCE,\angle DFC=\angle GCF$。
$\because CE$平分$\angle BCA,CF$平分$\angle ACG$，
$\therefore \angle BCE=\angle DCE,\angle DCF=\angle GCF$，
$\therefore \angle DEC=\angle DCE,\angle DFC=\angle DCF$，
$\therefore DE=DC,DF=DC$，
$\therefore DE=DF$。
$\because$点$D$是边$AC$的中点，
$\therefore AD=CD$，
$\therefore$四边形$AECF$是平行四边形。
$\because \angle BCA+\angle ACG=180^{\circ}$，
$\therefore \angle ECF=\angle DCE+\angle DCF=\frac{1}{2}\times 180^{\circ}=90^{\circ}$，
$\therefore$平行四边形$AECF$是矩形。

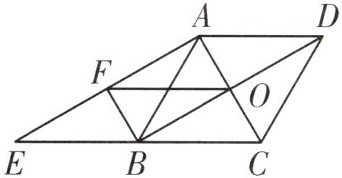
9. 如图，在菱形$ABCD$中，对角线$AC$，$BD$相交于点$O$，延长$CB$到点$E$，使得$BE=BC$，连接$AE$，过点$B$作$BF// AC$，交$AE$于点$F$，连接$OF$。
（1）求证：四边形$AFBO$是矩形；
（2）若$\angle E=30^{\circ}$，$OF=2$，求菱形$ABCD$的面积。

（1）证明：$\because$四边形$ABCD$是菱形，
$\therefore AD// BC,AC\perp BD,AD=BC$，
$\because BE=BC$，
$\therefore AD=BE$，
$\therefore$四边形$AEBD$是平行四边形，
$\therefore AE// BD$。
$\because BF// AC$，
$\therefore$四边形$AFBO$是平行四边形。
$\because AC\perp BD,AE// BD$，
$\therefore AE\perp AC$，
$\therefore \angle OAF=90^{\circ}$，
$\therefore$平行四边形$AFBO$是矩形。
（2）解：由(1)知四边形$AFBO$是矩形，
$\therefore \angle FAO=90^{\circ},OF=AB=2$，
在$Rt\triangle AEC$中，$BE=BC$，
$\therefore AB=BE=BC=2$，
又$\because \angle E=30^{\circ}$，
$\therefore \angle ACB=60^{\circ}$，
$\therefore \triangle ABC$为等边三角形，
$\therefore S_{菱形ABCD}=2S_{\triangle ABC}=2× \frac{1}{2}× 2× 2× \frac{\sqrt{3}}{2}=$$2\sqrt{3}$。

答案：
(1) 证明：$\because$四边形$ABCD$是菱形，
$\therefore AD// BC,AC\perp BD,AD=BC$，
$\because BE=BC$，
$\therefore AD=BE$，
$\therefore$四边形$AEBD$是平行四边形，
$\therefore AE// BD$。
$\because BF// AC$，
$\therefore$四边形$AFBO$是平行四边形。
$\because AC\perp BD,AE// BD$，
$\therefore AE\perp AC$，
$\therefore \angle OAF=90^{\circ}$，
$\therefore$平行四边形$AFBO$是矩形。
(2) 解：由
(1)知四边形$AFBO$是矩形，
$\therefore \angle FAO=90^{\circ},OF=AB=2$，
在$Rt\triangle AEC$中，$BE=BC$，
$\therefore AB=BE=BC=2$，
又$\because \angle E=30^{\circ}$，
$\therefore \angle ACB=60^{\circ}$，
$\therefore \triangle ABC$为等边三角形，
$\therefore S_{菱形ABCD}=2S_{\triangle ABC}=2\times \frac{1}{2}\times 2\times 2\times \frac{\sqrt{3}}{2}=2\sqrt{3}$。