1. 在平面中,下列命题为真命题的是 (
A. 四边相等的四边形是正方形
B. 对角线相等的四边形是菱形
C. 四个角相等的四边形是矩形
D. 对角线互相垂直的四边形是平行四边形
C
)A. 四边相等的四边形是正方形
B. 对角线相等的四边形是菱形
C. 四个角相等的四边形是矩形
D. 对角线互相垂直的四边形是平行四边形
答案:
C
2. 如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是 (
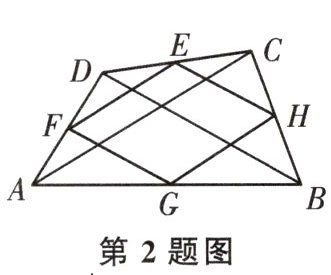
A. $ AB // DC $
B. $ AC = BD $
C. $ AC \perp BD $
D. $ AB = DC $
C
)
A. $ AB // DC $
B. $ AC = BD $
C. $ AC \perp BD $
D. $ AB = DC $
答案:
C
3. 如图,将两条宽度均为2的纸条相交成$ 30^{\circ} $的角叠放,则重合部分构成的四边形ABCD的面积为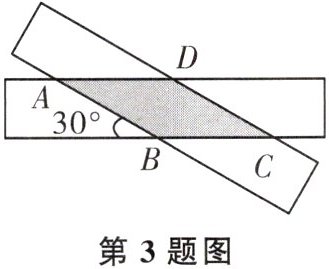
8
。
答案:
8
4. 把一张矩形纸片(矩形ABCD)按如图所示的方式折叠,使点B和点D重合,折痕为EF,若$ AB = 3 \mathrm{cm} $, $ BC = 5 \mathrm{cm} $,则重叠部分($ \triangle DEF $)的面积是
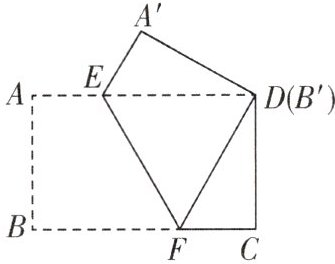
5.1
$ \mathrm{cm}^{2} $。
答案:
5.1 解析:由折叠的性质,可得$A'B'=AB$,$A'E=AE$。在$Rt\triangle A'DE$中,有$A'D^{2}+A'E^{2}=DE^{2}$。又$AE + DE = AD$,可设$DE = x cm$,则$A'E = AD - DE = (5 - x)cm$,列方程,得$3^{2}+(5 - x)^{2}=x^{2}$,解得$x = 3.4$,即$DE = 3.4cm$,所以$S_{\triangle DEF}=\frac{1}{2}DE\cdot AB=\frac{1}{2}×3.4×3 = 5.1(cm^{2})$。
5. 如图,在菱形ABCD中,E,F分别是BC和DC边上的点,且$ EC = FC $。求证:$ \angle AEF = \angle AFE $。
证明:∵四边形$ABCD$是菱形,
∴$AB = AD = BC = DC$,$∠B = ∠D$。
∵$EC = FC$,
∴$BE = DF$。
在$\triangle ABE$和$\triangle ADF$中,$\begin{cases}AB = AD\\∠B = ∠D\\BE = DF\end{cases}$
∴$\triangle ABE≌\triangle ADF$(
∴$AE = AF$,
∴$∠AEF = ∠AFE$。
证明:∵四边形$ABCD$是菱形,
∴$AB = AD = BC = DC$,$∠B = ∠D$。
∵$EC = FC$,
∴$BE = DF$。
在$\triangle ABE$和$\triangle ADF$中,$\begin{cases}AB = AD\\∠B = ∠D\\BE = DF\end{cases}$
∴$\triangle ABE≌\triangle ADF$(
SAS
),∴$AE = AF$,
∴$∠AEF = ∠AFE$。
答案:
证明:
∵四边形$ABCD$是菱形,
∴$AB = AD = BC = DC$,$∠B = ∠D$。
∵$EC = FC$,
∴$BE = DF$。
在$\triangle ABE$和$\triangle ADF$中,$\begin{cases}AB = AD\\∠B = ∠D\\BE = DF\end{cases}$
∴$\triangle ABE≌\triangle ADF(SAS)$,
∴$AE = AF$,
∴$∠AEF = ∠AFE$。
∵四边形$ABCD$是菱形,
∴$AB = AD = BC = DC$,$∠B = ∠D$。
∵$EC = FC$,
∴$BE = DF$。
在$\triangle ABE$和$\triangle ADF$中,$\begin{cases}AB = AD\\∠B = ∠D\\BE = DF\end{cases}$
∴$\triangle ABE≌\triangle ADF(SAS)$,
∴$AE = AF$,
∴$∠AEF = ∠AFE$。
6. 如图,AC是矩形ABCD的对角线,EF平分AC,且分别交AD,AC,BC于点E,O,F,求证:$ ED = BF $。
证明:∵$EF$平分$AC$,
∴
∵四边形$ABCD$为矩形,
∴
∴
又∵
∴
∴
∴$DE = BF$。
证明:∵$EF$平分$AC$,
∴
$AO = OC$
。∵四边形$ABCD$为矩形,
∴
$AD = BC$
,$AD// BC$
,∴
$∠EAO = ∠FCO$
。又∵
$∠AOE = ∠COF$
,∴
$\triangle AOE≌\triangle COF(ASA)$
,∴
$AE = CF$
,∴$DE = BF$。
答案:
证明:
∵$EF$平分$AC$,
∴$AO = OC$。
∵四边形$ABCD$为矩形,
∴$AD = BC$,$AD// BC$,
∴$∠EAO = ∠FCO$。
又
∵$∠AOE = ∠COF$,
∴$\triangle AOE≌\triangle COF(ASA)$,
∴$AE = CF$,
∴$DE = BF$。
∵$EF$平分$AC$,
∴$AO = OC$。
∵四边形$ABCD$为矩形,
∴$AD = BC$,$AD// BC$,
∴$∠EAO = ∠FCO$。
又
∵$∠AOE = ∠COF$,
∴$\triangle AOE≌\triangle COF(ASA)$,
∴$AE = CF$,
∴$DE = BF$。
7. 如图,在$ \triangle ABC $中,AD平分$ \angle BAC $,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F。求证:四边形AEDF是菱形。
证明:∵$DE// AC$,$DF// AB$,
∴四边形$AEDF$是
∵$AD$平分$∠BAC$,
∴$∠EAD = ∠FAD$。
∵$DF// AB$,
∴$∠EAD = ∠FDA$,
∴$∠FAD = ∠FDA$,
∴$AF = FD$,
∴四边形$AEDF$是
证明:∵$DE// AC$,$DF// AB$,
∴四边形$AEDF$是
平行四边形
。∵$AD$平分$∠BAC$,
∴$∠EAD = ∠FAD$。
∵$DF// AB$,
∴$∠EAD = ∠FDA$,
∴$∠FAD = ∠FDA$,
∴$AF = FD$,
∴四边形$AEDF$是
菱形
。
答案:
解:
∵$DE// AC$,$DF// AB$,
∴四边形$AEDF$是平行四边形。
∵$AD$平分$∠BAC$,
∴$∠EAD = ∠FAD$。
∵$DF// AB$,
∴$∠EAD = ∠FDA$,
∴$∠FAD = ∠FDA$,
∴$AF = FD$,
∴四边形$AEDF$是菱形。
∵$DE// AC$,$DF// AB$,
∴四边形$AEDF$是平行四边形。
∵$AD$平分$∠BAC$,
∴$∠EAD = ∠FAD$。
∵$DF// AB$,
∴$∠EAD = ∠FDA$,
∴$∠FAD = ∠FDA$,
∴$AF = FD$,
∴四边形$AEDF$是菱形。
8. 如图,在$ \triangle ABC $中,$ AB = AC = 5 $, $ BC = 6 $,AD是BC边上的中线,四边形ADBE是平行四边形。求证:四边形ADBE是矩形。
证明:∵$AB = AC$,$AD$是$BC$边上的中线,
∴
∴$∠ADB = 90^{\circ}$。
∵四边形$ADBE$是平行四边形,
∴
证明:∵$AB = AC$,$AD$是$BC$边上的中线,
∴
$AD⊥BC$
,∴$∠ADB = 90^{\circ}$。
∵四边形$ADBE$是平行四边形,
∴
平行四边形ADBE
是矩形。
答案:
证明:
∵$AB = AC$,$AD$是$BC$边上的中线,
∴$AD⊥BC$,
∴$∠ADB = 90^{\circ}$。
∵四边形$ADBE$是平行四边形,
∴$\square ADBE$是矩形。
∵$AB = AC$,$AD$是$BC$边上的中线,
∴$AD⊥BC$,
∴$∠ADB = 90^{\circ}$。
∵四边形$ADBE$是平行四边形,
∴$\square ADBE$是矩形。
查看更多完整答案,请扫码查看


