《2025年春如金卷课时作业AB本九年级数学上册北师大版》

4. 如果两个相似三角形对应中线的比是9:4，那么它们对应角平分线的比为 (A)
A. 9:4
B. 81:16
C. 16:81
D. 2:3

答案： A

5. 已知两个相似三角形，其中一组对应边上的高分别是2和6，那么这两个三角形的相似比为 (B)
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{1}{6}$

答案： B

6. 如果△ABC∽△DEF(其中顶点A，B，C依次与顶点D，E，F对应)那么下列等式中，不一定成立的是 (C)
A. ∠A=∠D
B. $\frac{∠A}{∠B}=\frac{∠D}{∠E}$
C. AB=DE
D. $\frac{AB}{AC}=\frac{DE}{DF}$

答案： C

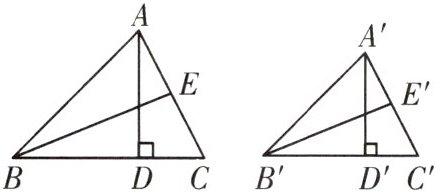
7. 如图，△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，且AD=4，A′D′=3，BE=6，则B′E′的长为$\frac{9}{2}$。

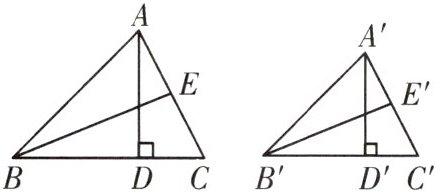
答案： $\frac{9}{2}$

8. 如图，在矩形ABCD中，点EF分别在边AD，DC上，△ABE∽△DEF，AB=6，AE=9，DE=2。
(1)求EF的长。$\sqrt{13}$
(2)求证：∠BEF=90°。
证明：∵△ABE∽△DEF，
∴∠ABE=∠DEF，
∵在Rt△ABE中，∠ABE+∠AEB=90°，
∴∠DEF+∠AEB=90°，
∴∠BEF=90°。

答案：
(1) 解：$\because \triangle ABE\backsim\triangle DEF$，
$\therefore \frac{AB}{DE}=\frac{AE}{DF}$，
$\because AB=6$，$AE=9$，$DE=2$，
$\therefore \frac{6}{2}=\frac{9}{DF}$，
$\therefore DF=3$，
$\because$ 矩形 $ABCD$，
$\therefore \angle EDF=90^{\circ}$，
$\therefore$ 在 $Rt\triangle DEF$ 中，
$EF=\sqrt{DE^{2}+DF^{2}}=\sqrt{2^{2}+3^{2}}=\sqrt{13}$；
(2) 证明：$\because \triangle ABE\backsim\triangle DEF$，
$\therefore \angle ABE=\angle DEF$，
$\because$ 在 $Rt\triangle ABE$ 中，$\angle ABE+\angle AEB=90^{\circ}$，
$\therefore \angle DEF+\angle AEB=90^{\circ}$，
$\therefore \angle BEF=90^{\circ}$。

9. 阅读理解：
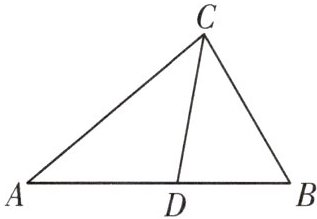
从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫作这个三角形的完美分割线。
(1)如图，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线。
(2)在△ABC中，∠A=48°，CD为△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数。

答案：

(1) 证明：$\because \angle A=40^{\circ}$，$\angle B=60^{\circ}$，
$\therefore \angle ACB=180^{\circ}-\angle A-\angle B=80^{\circ}$，
$\because \angle A\neq\angle B\neq\angle ACB$，
$\therefore \triangle ABC$ 不是等腰三角形。
$\because CD$ 平分 $\angle ACB$，
$\therefore \angle ACD=\angle BCD=\frac{1}{2}\angle ACB=40^{\circ}$，
$\therefore \angle ACD=\angle A=40^{\circ}$，
$\therefore \triangle ACD$ 为等腰三角形。
$\therefore \angle DCB=\angle A=40^{\circ}$，
$\because \angle CBD=\angle ABC$，
$\therefore \triangle BCD\backsim\triangle BAC$，
$\therefore CD$ 是 $\triangle ABC$ 的完美分割线。
(2) 解：① 如图 3 所示，
当 $AD=CD$ 时，$\angle ACD=\angle A=48^{\circ}$，
根据完美分割线的定义，可得 $\triangle BDC\backsim\triangle BCA$，
$\therefore \angle BCD=\angle A=48^{\circ}$，则 $\angle ACB=\angle ACD+\angle BCD=96^{\circ}$。
② 如图 4 所示，
当 $AD=AC$ 时，$\angle ACD=\angle ADC=\frac{180^{\circ}-48^{\circ}}{2}=66^{\circ}$，
根据完美分割线的定义，可得 $\triangle BDC\backsim\triangle BCA$，
$\therefore \angle BCD=\angle A=48^{\circ}$，
$\therefore \angle ACB=\angle ACD+\angle BCD=114^{\circ}$。

③ 如图 5 所示，
当 $AC=CD$ 时，$\angle ADC=\angle A=48^{\circ}$。

$\because \triangle BDC\backsim\triangle BCA$，
$\therefore \angle BCD=\angle A=48^{\circ}$，
根据完美分割线的定义，可得 $\triangle BDC\backsim\triangle BCA$，
$\therefore \angle BCD=\angle A=48^{\circ}$，
$\therefore$ 这与 $\angle ADC＞\angle BCD$ 矛盾，
所以图 5 的情况不符合题意。
综上所述，$\angle ACB$ 的度数为 $96^{\circ}$ 或 $114^{\circ}$。