《2025年春如金卷课时作业AB本九年级数学上册北师大版》

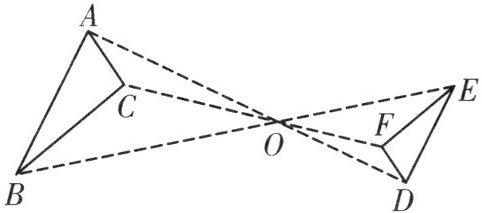
4. 如图，已知$\triangle ABC$与$\triangle DEF$位似，位似中心为点O，$\triangle ABC$的面积与$\triangle DEF$面积之比为$16:9$，则$CO:CF$的值为（B）

A. $3:4$
B. $4:7$
C. $4:3$
D. $7:4$

答案： B

5. 在平面直角坐标系中，已知点$A(-4,2)$，$B(-2,-2)$，以原点为位似中心，相似比为$1:2$，把$\triangle AOB$缩小，则点A的对应的坐标是（D）
A. $(-2,1)$
B. $(-8,4)$
C. $(-8,4)$或$(8,-4)$
D. $(-2,1)$或$(2,-1)$

答案： D

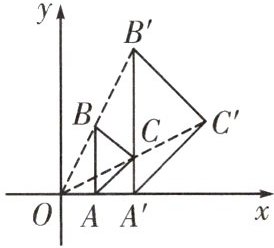
6. 如图，在平面直角坐标系中，等腰直角$\triangle A'B'C'$是等腰直角$\triangle ABC$以原点O为位似中心的位似图形，且位似比为$2:1$，点$A(1,0)$，$B(1,2)$，C在$A'B'$上，则点$C'$的坐标为（C）

A. $(2,4)$
B. $(2,2)$
C. $(4,2)$
D. $(4,4)$

答案： C

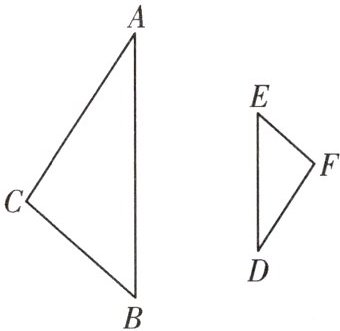
7. 如图，$\triangle DEF$是$\triangle ABC$经过位似变换得到的，位似中心是点O，请确定点O的位置，如果$OC=3.6cm$，$OF=2.4cm$，求它们的相似比。

答案：
解：如图，连接$AD$，$CF$交于点$O$，则点$O$即为所求。
$\because OC=3.6cm$，$OF=2.4cm$，
$\therefore OC:OF=3:2$，
$\therefore \triangle ABC$与$\triangle DEF$的相似比为$3:2$。

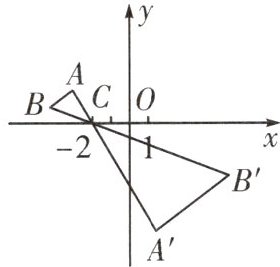
8. 如图所示，在$\triangle ABC$中，A，B两个顶点在x轴的上方，点C的坐标是$(-2,0)$。以点C为位似中心，在x轴的下方作$\triangle ABC$的位似图形$\triangle A'B'C$，并把$\triangle ABC$的边长放大到原来的2倍，设点B的对应点$B'$的横坐标是m，则点B的横坐标是（B）

A. $-\frac{m+2}{2}$
B. $-\frac{m+6}{2}$
C. $-\frac{m-6}{2}$
D. $-\frac{m-2}{2}$

答案： B 解析：设点$B$的横坐标为$x$，则$B$，$C$间的横坐标的长度为$-2 - x$，$B'$，$C$间的横坐标的长度为$m + 2$。
$\because \triangle ABC$放大到原来的$2$倍得到$\triangle A'B'C$，
$\therefore 2(-2 - x)=m + 2$，解得：$x=-\frac{m + 6}{2}$。故选：B。

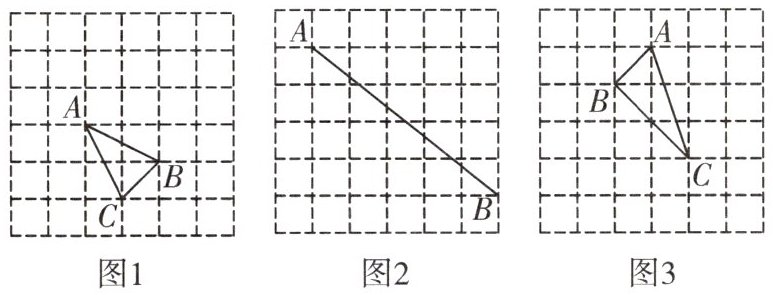
9. 如图，在正方形网格中，点A，B，C都在格点上，利用格点按要求完成下列作图。（要求仅用无刻度的直尺，不要求写画法，保留必要的作图痕迹）
（1）在图1中，以C为位似中心，相似比为$1:2$，在格点上将$\triangle ABC$放大得到$\triangle A_1B_1C_1$，请画出$\triangle A_1B_1C_1$；
（2）在图2中，线段AB上作点M，利用格点作图使得$\frac{AM}{BM}=\frac{3}{2}$；
（3）在图3中，利用格点在AC边上作一个点D，使得$\triangle ABD \backsim \triangle ACB$。

答案：
解：
(1)如图 1，$\triangle A_1B_1C_1$为所作；
(2)如图 2，点$M$为所作；
(3)如图 3，点$D$为所作。