9. 如图,在$ □ ABCD $中,$ BD \perp AB $,延长AB至点E,使$ BE = AB $,连接EC。
(1)求证:四边形BECD是矩形;
(2)连接AC,若$ AD = 3 $, $ CD = 2 $,求AC的长为
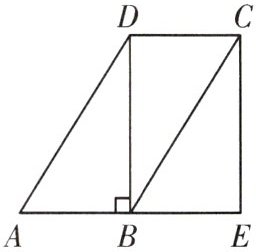
(1)求证:四边形BECD是矩形;
(2)连接AC,若$ AD = 3 $, $ CD = 2 $,求AC的长为
$\sqrt{21}$
。
答案:
(1) 证明:
∵四边形$ABCD$是平行四边形,
∴$CD = AB$,$CD// AB$,
又
∵$BE = AB$,
∴$BE = DC$,$BE// CD$,
∴四边形$BECD$为平行四边形。
∵$BD⊥AB$,
∴$∠ABD = ∠DBE = 90^{\circ}$,
∴平行四边形$BECD$是矩形;
(2) 解:如图,
∵四边形$ABCD$是平行四边形,
∴$BC = AD = 3$,$AB = CD = 2$。
由
(1)可知,四边形$BECD$是矩形,
∴$∠E = 90^{\circ}$,$BE = CD = 2$,
∴$AE = AB + BE = 4$。
在$Rt\triangle BCE$中,由勾股定理得:
$CE = \sqrt{BC^{2}-BE^{2}}=\sqrt{3^{2}-2^{2}}=\sqrt{5}$,
∴$AC = \sqrt{AE^{2}+CE^{2}}=\sqrt{4^{2}+(\sqrt{5})^{2}}=\sqrt{21}$,即$AC$的长为$\sqrt{21}$。
(1) 证明:
∵四边形$ABCD$是平行四边形,
∴$CD = AB$,$CD// AB$,
又
∵$BE = AB$,
∴$BE = DC$,$BE// CD$,
∴四边形$BECD$为平行四边形。
∵$BD⊥AB$,
∴$∠ABD = ∠DBE = 90^{\circ}$,
∴平行四边形$BECD$是矩形;
(2) 解:如图,
∵四边形$ABCD$是平行四边形,
∴$BC = AD = 3$,$AB = CD = 2$。
由
(1)可知,四边形$BECD$是矩形,
∴$∠E = 90^{\circ}$,$BE = CD = 2$,
∴$AE = AB + BE = 4$。
在$Rt\triangle BCE$中,由勾股定理得:
$CE = \sqrt{BC^{2}-BE^{2}}=\sqrt{3^{2}-2^{2}}=\sqrt{5}$,
∴$AC = \sqrt{AE^{2}+CE^{2}}=\sqrt{4^{2}+(\sqrt{5})^{2}}=\sqrt{21}$,即$AC$的长为$\sqrt{21}$。
10. 如图,在正方形ABCD中,点E为CD的中点,连接AE并延长交BC的延长线于点G,点F在BC上,$ \angle FAE = \angle DAE $,连接FE并延长交AD的延长线于点H,连接HG。
(1)求证:四边形AFGH为菱形;
(2)若正方形ABCD的边长为4,求四边形AFGH的面积。
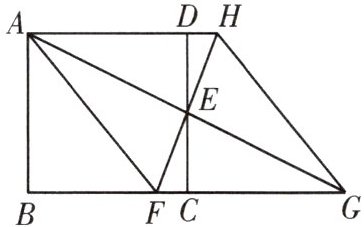
(1) 证明:∵四边形$ABCD$是正方形,
∴$AD// BC$,
∴$∠DAE = ∠FGA$,
又∵$∠FAE = ∠DAE$,
∴$∠FGA = ∠FAE$,
∴$FA = FG$。
∵点$E$为$CD$的中点,
∴$DE = CE$。
在$\triangle ADE$和$\triangle GCE$中,$\begin{cases}∠DAE = ∠EGC\\∠ADE = ∠GCE\\DE = CE\end{cases}$
∴$\triangle ADE≌\triangle GCE$(
∴$AD = CG$,
同理:$\triangle DEH≌\triangle CEF$(
∴$DH = CF$。
∵$AH = AD + DH$,$GF = CG + CF$,
∴$AH = FG$,
又∵$AH// FG$,
∴四边形$AFGH$为平行四边形,
∵$FA = FG$,
∴四边形$AFGH$为菱形。
(2) 解:设$FC = x$,由(1)知$FC = DH = x$,
∴$AF = AH = AD + DH = 4 + x$,$BF = BC - FC = 4 - x$。
在$Rt\triangle ABF$中,根据勾股定理,得$AF^{2}=AB^{2}+BF^{2}$,
∴$(4 + x)^{2}=4^{2}+(4 - x)^{2}$,解得$x = $
∴$AF = FG = 4 + x = $
∴菱形$AFGH$的面积为
(1)求证:四边形AFGH为菱形;
(2)若正方形ABCD的边长为4,求四边形AFGH的面积。

(1) 证明:∵四边形$ABCD$是正方形,
∴$AD// BC$,
∴$∠DAE = ∠FGA$,
又∵$∠FAE = ∠DAE$,
∴$∠FGA = ∠FAE$,
∴$FA = FG$。
∵点$E$为$CD$的中点,
∴$DE = CE$。
在$\triangle ADE$和$\triangle GCE$中,$\begin{cases}∠DAE = ∠EGC\\∠ADE = ∠GCE\\DE = CE\end{cases}$
∴$\triangle ADE≌\triangle GCE$(
AAS
),∴$AD = CG$,
同理:$\triangle DEH≌\triangle CEF$(
AAS
),∴$DH = CF$。
∵$AH = AD + DH$,$GF = CG + CF$,
∴$AH = FG$,
又∵$AH// FG$,
∴四边形$AFGH$为平行四边形,
∵$FA = FG$,
∴四边形$AFGH$为菱形。
(2) 解:设$FC = x$,由(1)知$FC = DH = x$,
∴$AF = AH = AD + DH = 4 + x$,$BF = BC - FC = 4 - x$。
在$Rt\triangle ABF$中,根据勾股定理,得$AF^{2}=AB^{2}+BF^{2}$,
∴$(4 + x)^{2}=4^{2}+(4 - x)^{2}$,解得$x = $
1
,∴$AF = FG = 4 + x = $
5
,∴菱形$AFGH$的面积为
20
。
答案:
(1) 证明:
∵四边形$ABCD$是正方形,
∴$AD// BC$,
∴$∠DAE = ∠FGA$,
又
∵$∠FAE = ∠DAE$,
∴$∠FGA = ∠FAE$,
∴$FA = FG$。
∵点$E$为$CD$的中点,
∴$DE = CE$。
在$\triangle ADE$和$\triangle GCE$中,$\begin{cases}∠DAE = ∠EGC\\∠ADE = ∠GCE\\DE = CE\end{cases}$
∴$\triangle ADE≌\triangle GCE(AAS)$,
∴$AD = CG$,
同理:$\triangle DEH≌\triangle CEF(AAS)$,
∴$DH = CF$。
∵$AH = AD + DH$,$GF = CG + CF$,
∴$AH = FG$,
又
∵$AH// FG$,
∴四边形$AFGH$为平行四边形,
∵$FA = FG$,
∴四边形$AFGH$为菱形。
(2) 解:设$FC = x$,由
(1)知$FC = DH = x$,
∴$AF = AH = AD + DH = 4 + x$,$BF = BC - FC = 4 - x$。
在$Rt\triangle ABF$中,根据勾股定理,得$AF^{2}=AB^{2}+BF^{2}$,
∴$(4 + x)^{2}=4^{2}+(4 - x)^{2}$,解得$x = 1$,
∴$AF = FG = 4 + x = 5$,
∴菱形$AFGH$的面积为$FG\cdot DC = 5×4 = 20$。
(1) 证明:
∵四边形$ABCD$是正方形,
∴$AD// BC$,
∴$∠DAE = ∠FGA$,
又
∵$∠FAE = ∠DAE$,
∴$∠FGA = ∠FAE$,
∴$FA = FG$。
∵点$E$为$CD$的中点,
∴$DE = CE$。
在$\triangle ADE$和$\triangle GCE$中,$\begin{cases}∠DAE = ∠EGC\\∠ADE = ∠GCE\\DE = CE\end{cases}$
∴$\triangle ADE≌\triangle GCE(AAS)$,
∴$AD = CG$,
同理:$\triangle DEH≌\triangle CEF(AAS)$,
∴$DH = CF$。
∵$AH = AD + DH$,$GF = CG + CF$,
∴$AH = FG$,
又
∵$AH// FG$,
∴四边形$AFGH$为平行四边形,
∵$FA = FG$,
∴四边形$AFGH$为菱形。
(2) 解:设$FC = x$,由
(1)知$FC = DH = x$,
∴$AF = AH = AD + DH = 4 + x$,$BF = BC - FC = 4 - x$。
在$Rt\triangle ABF$中,根据勾股定理,得$AF^{2}=AB^{2}+BF^{2}$,
∴$(4 + x)^{2}=4^{2}+(4 - x)^{2}$,解得$x = 1$,
∴$AF = FG = 4 + x = 5$,
∴菱形$AFGH$的面积为$FG\cdot DC = 5×4 = 20$。
11. 问题引入:如图1,$ AB // CD $, $ AB > CD $, $ \angle ABD = 90^{\circ} $,E是线段AC的中点。连接DE并延长交AB于点F,连接BE。则BE与DE之间的数量关系是
问题延伸:如图2,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,点G在BC上,P是线段DF的中点,连接PC,PG。
(1)判断PC与PG之间的数量关系,并说明理由;
(2)连接CF,若$ AB = 3 $, $ PC = \sqrt{2} $,则CF的长为
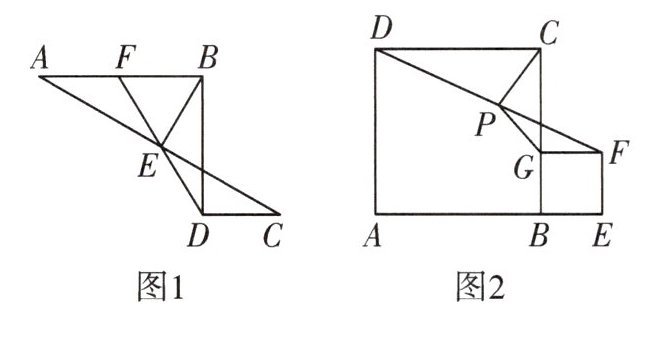
$BE = DE$
。问题延伸:如图2,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,点G在BC上,P是线段DF的中点,连接PC,PG。
(1)判断PC与PG之间的数量关系,并说明理由;
(2)连接CF,若$ AB = 3 $, $ PC = \sqrt{2} $,则CF的长为
$\sqrt{5}$
。
答案:
问题引入:$BE = DE$,理由如下:
∵$AB// CD$,
∴$∠A = ∠C$。
∵$E$是$AC$的中点,
∴$AE = CE$。
在$\triangle AEF$和$\triangle CED$中,$\begin{cases}∠A = ∠C\\AE = CE\\∠AEF = ∠CED\end{cases}$
∴$\triangle AEF≌\triangle CED(ASA)$,
∴$EF = DE$。
∵$∠ABD = 90^{\circ}$,
∴$BE$为$Rt\triangle BDF$斜边上的中线,
∴$EF = DE = BE$,
∴$BE = DE$。
故答案为:$BE = DE$;
问题延伸:
(1)$PC = PG$,理由如下:
如图,延长$GP$交$CD$于点$M$,
∵四边形$ABCD$,$BEFG$为正方形,
∴$CD// AE// GF$,$∠BCD = 90^{\circ}$,
∴$∠CDP = ∠PFG$。
∵$P$为$DF$的中点,
∴$DP = FP$。
在$\triangle DPM$和$\triangle FPG$中,
$\begin{cases}∠MDP = ∠GFP\\DP = FP\\∠DPM = ∠FPG\end{cases}$
∴$\triangle DPM≌\triangle FPG(ASA)$,
∴$PM = PG$,$GF = DM$。
∵$PC$为$Rt\triangle MCG$斜边上的中线,
∴$PC = PG = PM$,
∴$PC = PG$;
(2)
∵四边形$ABCD$,$BEFG$为正方形,
∴$AB = BC = CD = 3$,$BG = GF = DM$,$∠CGF = 90^{\circ}$。
设$BG = GF = DM = x$,
∴$CM = CG = 3 - x$。
∵$PC = PG = PM = \sqrt{2}$,
∴$MG = 2\sqrt{2}$。
∵$MC^{2}+CG^{2}=MG^{2}$,
∴$(3 - x)^{2}+(3 - x)^{2}=(2\sqrt{2})^{2}$,
∴$x = 1$,
∴$GF = 1$,$CG = 3 - 1 = 2$,
∴$CF = \sqrt{GF^{2}+CG^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。
∵$AB// CD$,
∴$∠A = ∠C$。
∵$E$是$AC$的中点,
∴$AE = CE$。
在$\triangle AEF$和$\triangle CED$中,$\begin{cases}∠A = ∠C\\AE = CE\\∠AEF = ∠CED\end{cases}$
∴$\triangle AEF≌\triangle CED(ASA)$,
∴$EF = DE$。
∵$∠ABD = 90^{\circ}$,
∴$BE$为$Rt\triangle BDF$斜边上的中线,
∴$EF = DE = BE$,
∴$BE = DE$。
故答案为:$BE = DE$;
问题延伸:
(1)$PC = PG$,理由如下:
如图,延长$GP$交$CD$于点$M$,
∵四边形$ABCD$,$BEFG$为正方形,
∴$CD// AE// GF$,$∠BCD = 90^{\circ}$,
∴$∠CDP = ∠PFG$。
∵$P$为$DF$的中点,
∴$DP = FP$。
在$\triangle DPM$和$\triangle FPG$中,
$\begin{cases}∠MDP = ∠GFP\\DP = FP\\∠DPM = ∠FPG\end{cases}$
∴$\triangle DPM≌\triangle FPG(ASA)$,
∴$PM = PG$,$GF = DM$。
∵$PC$为$Rt\triangle MCG$斜边上的中线,
∴$PC = PG = PM$,
∴$PC = PG$;
(2)
∵四边形$ABCD$,$BEFG$为正方形,
∴$AB = BC = CD = 3$,$BG = GF = DM$,$∠CGF = 90^{\circ}$。
设$BG = GF = DM = x$,
∴$CM = CG = 3 - x$。
∵$PC = PG = PM = \sqrt{2}$,
∴$MG = 2\sqrt{2}$。
∵$MC^{2}+CG^{2}=MG^{2}$,
∴$(3 - x)^{2}+(3 - x)^{2}=(2\sqrt{2})^{2}$,
∴$x = 1$,
∴$GF = 1$,$CG = 3 - 1 = 2$,
∴$CF = \sqrt{GF^{2}+CG^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。
查看更多完整答案,请扫码查看


