4. 下列关系中,是菱形的性质但不是平行四边形的性质的是 (
A. 对角线垂直
B. 两组对边分别平行
C. 对角线互相平分
D. 两组对角分别相等
A
)A. 对角线垂直
B. 两组对边分别平行
C. 对角线互相平分
D. 两组对角分别相等
答案:
A
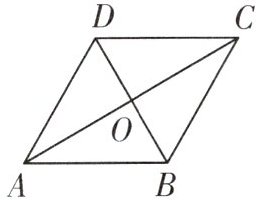
5. 如图,在菱形ABCD中,对角线AC与BD相交于点O,$∠ABC=120^{\circ }$,$BD=4$,则对角线AC的长为 (
A. $4\sqrt {3}$
B. $2\sqrt {3}$
C. 4
D. 8
A
)
A. $4\sqrt {3}$
B. $2\sqrt {3}$
C. 4
D. 8
答案:
A
6. 如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB,AD的垂线段PE,PF,则$PE+PF$等于

3
。
答案:
3
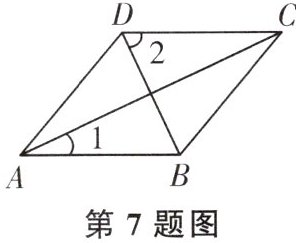
7. 如图,在菱形ABCD中,连接AC,BD,若$∠1=25^{\circ }$,则$∠2$的度数为
$65^{\circ}$
。
答案:
$65^{\circ}$
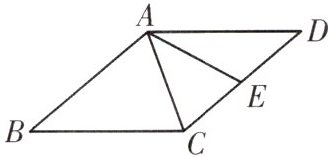
8. 如图,在菱形ABCD中,$∠B=40^{\circ }$,点E在CD上,$AE=AC$,则$∠BAE=$
$110^{\circ}$
。
答案:
$110^{\circ}$
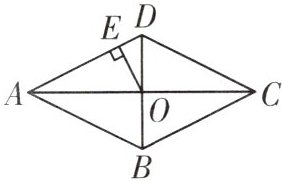
9. 如图,菱形ABCD的对角线AC,BD相交于点O,$OE\perp AD$,垂足为E,$AC=16$,$BD=12$,求AD,OE的长。
AD的长为

AD的长为
10
,OE的长为$\frac{24}{5}$
。
答案:
解:
∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,
∴AO⊥DO,$AO=\frac {1}{2}AC=8$,$DO=\frac {1}{2}BD=6$,
∴$AD=\sqrt {AO^{2}+OD^{2}}=10$。
∵OE⊥AD,
∴$S_{△ADO}=\frac {1}{2}AD×OE=\frac {1}{2}AO×OD$,
∴$OE=\frac {AO×OD}{AD}=\frac {6×8}{10}=\frac {24}{5}$。
∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,
∴AO⊥DO,$AO=\frac {1}{2}AC=8$,$DO=\frac {1}{2}BD=6$,
∴$AD=\sqrt {AO^{2}+OD^{2}}=10$。
∵OE⊥AD,
∴$S_{△ADO}=\frac {1}{2}AD×OE=\frac {1}{2}AO×OD$,
∴$OE=\frac {AO×OD}{AD}=\frac {6×8}{10}=\frac {24}{5}$。
10. 如图,若菱形ABCD的面积为$2\sqrt {3}cm^{2}$,$∠A=120^{\circ }$,将菱形ABCD折叠,使点A恰好落在菱形对角线的交点O处,折痕为EF,则$EF=$
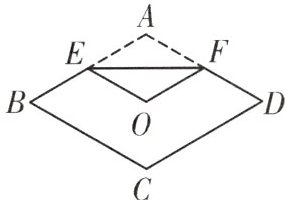
$\sqrt {3}$
cm。
答案:
$\sqrt {3}$
11. 如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,$∠ADF=∠CDE$。求证:$AE=CF$。
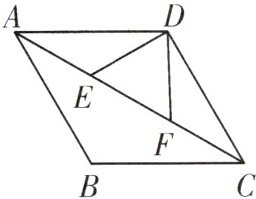
证明:∵四边形ABCD是菱形,E,F是对角线AC上两点,
∴
∵∠ADF=∠CDE,
∴∠ADF−∠EDF=∠CDE−∠EDF,
即
在△DAE和△DCF中,$\left\{\begin{array}{l} ∠DAC=∠DCA,\\ DA=DC,\\ ∠ADE=∠CDF,\end{array}\right.$
∴△DAE≌△DCF(
∴AE=CF。

证明:∵四边形ABCD是菱形,E,F是对角线AC上两点,
∴
DA=DC
,∠DAC=∠DCA
。∵∠ADF=∠CDE,
∴∠ADF−∠EDF=∠CDE−∠EDF,
即
∠ADE=∠CDF
。在△DAE和△DCF中,$\left\{\begin{array}{l} ∠DAC=∠DCA,\\ DA=DC,\\ ∠ADE=∠CDF,\end{array}\right.$
∴△DAE≌△DCF(
ASA
),∴AE=CF。
答案:
解:
∵四边形ABCD是菱形,E,F是对角线AC上两点,
∴DA=DC,∠DAC=∠DCA。
∵∠ADF=∠CDE,
∴∠ADF−∠EDF=∠CDE−∠EDF,
即∠ADE=∠CDF。
在△DAE和△DCF中,$\left\{\begin{array}{l} ∠DAC=∠DCA,\\ DA=DC,\\ ∠ADE=∠CDF,\end{array}\right.$
∴△DAE≌△DCF(ASA),
∴AE=CF。
∵四边形ABCD是菱形,E,F是对角线AC上两点,
∴DA=DC,∠DAC=∠DCA。
∵∠ADF=∠CDE,
∴∠ADF−∠EDF=∠CDE−∠EDF,
即∠ADE=∠CDF。
在△DAE和△DCF中,$\left\{\begin{array}{l} ∠DAC=∠DCA,\\ DA=DC,\\ ∠ADE=∠CDF,\end{array}\right.$
∴△DAE≌△DCF(ASA),
∴AE=CF。
12. 如图,在边长为1的菱形ABCD中,$∠DAB=60^{\circ }$,点M是AD上不同于A,D的一个动点,点N是CD上一动点,且$AM+CN=1$。
(1)证明:无论M,N怎样移动,$\triangle BMN$总是等边三角形;
(2)求$\triangle BMN$面积的最小值。
(1) 证明:如图所示,连接BD,
在菱形ABCD中,∠DAB=60°,
∴∠ADB=∠NDB=60°,故△ADB是等边三角形,
∴AB=BD,又AM+CN=1,DN+CN=1,∴AM=DN。
在△AMB和△DNB中,
$\left\{\begin{array}{l} AM=DN,\\ ∠MAB=∠NDB=60^{\circ },\\ AB=DB,\end{array}\right.$
∴△AMB≌△DNB(SAS),
∴BM=BN,∠MBA=∠NBD,
又∵∠MBA+∠DBM=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴△BMN是等边三角形。
(2) 解:过点B作BE⊥MN于点E。设BM=BN=MN=x,则$BE=\frac {\sqrt {3}}{2}x$,故$S_{△BMN}=\frac {1}{2}MN\cdot BE=\frac {\sqrt {3}}{4}x^{2}$,
∴当BM⊥AD时,x最小,此时,$x_{min}=\frac {\sqrt {3}}{2}$,$S_{min}=\frac {\sqrt {3}}{4}×(\frac {\sqrt {3}}{2})^{2}=$
∴△BMN面积的最小值为
(1)证明:无论M,N怎样移动,$\triangle BMN$总是等边三角形;
(2)求$\triangle BMN$面积的最小值。
(1) 证明:如图所示,连接BD,
在菱形ABCD中,∠DAB=60°,
∴∠ADB=∠NDB=60°,故△ADB是等边三角形,
∴AB=BD,又AM+CN=1,DN+CN=1,∴AM=DN。
在△AMB和△DNB中,
$\left\{\begin{array}{l} AM=DN,\\ ∠MAB=∠NDB=60^{\circ },\\ AB=DB,\end{array}\right.$
∴△AMB≌△DNB(SAS),
∴BM=BN,∠MBA=∠NBD,
又∵∠MBA+∠DBM=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴△BMN是等边三角形。
(2) 解:过点B作BE⊥MN于点E。设BM=BN=MN=x,则$BE=\frac {\sqrt {3}}{2}x$,故$S_{△BMN}=\frac {1}{2}MN\cdot BE=\frac {\sqrt {3}}{4}x^{2}$,
∴当BM⊥AD时,x最小,此时,$x_{min}=\frac {\sqrt {3}}{2}$,$S_{min}=\frac {\sqrt {3}}{4}×(\frac {\sqrt {3}}{2})^{2}=$
$\frac {3\sqrt {3}}{16}$
。∴△BMN面积的最小值为
$\frac {3\sqrt {3}}{16}$
。
答案:
(1) 证明:如图所示,连接BD,
在菱形ABCD中,∠DAB=60°,
∴∠ADB=∠NDB=60°,故△ADB是等边三角形,
∴AB=BD,又AM+CN=1,DN+CN=1,
∴AM=DN。
在△AMB和△DNB中,
$\left\{\begin{array}{l} AM=DN,\\ ∠MAB=∠NDB=60^{\circ },\\ AB=DB,\end{array}\right.$
∴△AMB≌△DNB(SAS),
∴BM=BN,∠MBA=∠NBD,
又
∵∠MBA+∠DBM=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴△BMN是等边三角形。
(2) 解:过点B作BE⊥MN于点E。设BM=BN=MN=x,则$BE=\frac {\sqrt {3}}{2}x$,故$S_{△BMN}=\frac {1}{2}MN\cdot BE=\frac {\sqrt {3}}{4}x^{2}$,
∴当BM⊥AD时,x最小,此时,$x_{min}=\frac {\sqrt {3}}{2}$,$S_{min}=\frac {\sqrt {3}}{4}×(\frac {\sqrt {3}}{2})^{2}=\frac {3\sqrt {3}}{16}$。
∴△BMN面积的最小值为$\frac {3\sqrt {3}}{16}$。
(1) 证明:如图所示,连接BD,
在菱形ABCD中,∠DAB=60°,
∴∠ADB=∠NDB=60°,故△ADB是等边三角形,
∴AB=BD,又AM+CN=1,DN+CN=1,
∴AM=DN。
在△AMB和△DNB中,
$\left\{\begin{array}{l} AM=DN,\\ ∠MAB=∠NDB=60^{\circ },\\ AB=DB,\end{array}\right.$
∴△AMB≌△DNB(SAS),
∴BM=BN,∠MBA=∠NBD,
又
∵∠MBA+∠DBM=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴△BMN是等边三角形。
(2) 解:过点B作BE⊥MN于点E。设BM=BN=MN=x,则$BE=\frac {\sqrt {3}}{2}x$,故$S_{△BMN}=\frac {1}{2}MN\cdot BE=\frac {\sqrt {3}}{4}x^{2}$,
∴当BM⊥AD时,x最小,此时,$x_{min}=\frac {\sqrt {3}}{2}$,$S_{min}=\frac {\sqrt {3}}{4}×(\frac {\sqrt {3}}{2})^{2}=\frac {3\sqrt {3}}{16}$。
∴△BMN面积的最小值为$\frac {3\sqrt {3}}{16}$。
查看更多完整答案,请扫码查看


