《2025年春如金卷课时作业AB本九年级数学上册北师大版》

1. 某反比例函数的图象过点$(-2,1)$，则此反比例函数解析式为（B）
A. $y=\frac{2}{x}$
B. $y=-\frac{2}{x}$
C. $y=\frac{1}{2x}$
D. $y=-\frac{1}{2x}$

答案： B

2. 下列各点中，在反比例函数$y=\frac{8}{x}$图象上的是（D）
A. $(-1,8)$
B. $(-2,4)$
C. $(1,7)$
D. $(2,4)$

答案： D

3. 下列各点中在反比例函数$y=-\frac{1}{x}$的图象上的是（D）
A. $(-2,1)$
B. $(1,-2)$
C. $(-\frac{1}{2},1)$
D. $(\frac{1}{2},-2)$

答案： D

4. 已知点$A(-1,y_{1})$，$B(2,y_{2})$，$C(4,y_{3})$都在反比例函数$y=-\frac{5}{x}$的图象上，则下列结论中正确的是（B）
A. $y_{1}＜y_{2}＜y_{3}$
B. $y_{2}＜y_{3}＜y_{1}$
C. $y_{1}＜y_{3}＜y_{2}$
D. $y_{3}＜y_{2}＜y_{1}$

答案： B

5. 已知点$(-1,y_{1})$，$(-2,y_{2})$，$(3,y_{3})$在反比例函数$y=\frac{k}{x}(k＜0)$的图象上，下列结论正确的是（B）
A. $y_{1}＞y_{3}＞y_{2}$
B. $y_{1}＞y_{2}＞y_{3}$
C. $y_{3}＞y_{1}＞y_{2}$
D. $y_{3}＞y_{2}＞y_{1}$

答案： B

6. 已知一次函数$y_{1}=k_{1}x-b$与反比例函数$y_{2}=\frac{k_{2}}{x}$在同一平面直角坐标系中的图象如图所示，则当$k_{1}x＜\frac{k_{2}}{x}+b$时，$x$的取值范围是（B）

A. $x＜-1$或$0＜x＜3$
B. $-1＜x＜0$或$x＞3$
C. $-3＜x＜0$或$x＞1$
D. $x＞3$

答案： B

7. 已知某品牌显示器的使用寿命为定值。这种显示器可工作的天数$y$与平均每天工作的时长$x$是反比例函数关系，图象如图所示，如果这种显示器至少要用2000天，那么显示器平均每天工作的时长$x$应控制在（A）

A. $0＜x\leqslant10$
B. $10\leqslant x\leqslant24$
C. $0＜x\leqslant20$
D. $20\leqslant x\leqslant24$

答案： A

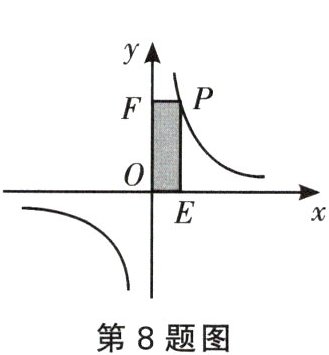
8. 如图，点$P$是反比例函数$y=\frac{6}{x}$图象上的一点，则矩形$PEOF$的面积是6。

答案： 6

9. 反比例函数$y=\frac{k}{x}$的图象如图所示，点$A$是该函数图象上一点，$AB\perp x$轴，垂足是$B$，若$S_{\triangle AOB}=1$，则$k$的值为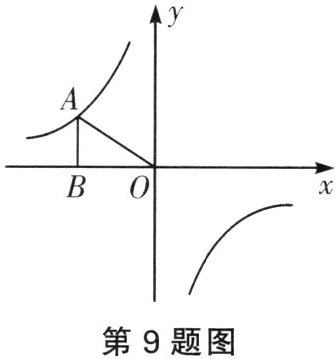-2。

答案： -2

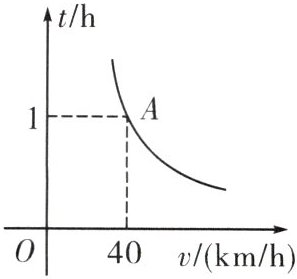
10. 如图，一辆汽车匀速通过某段公路，所需时间$t(h)$与行驶速度$v(km/h)$的函数图象为双曲线的一段，若这段公路行驶速度不得超过80km/h，则该汽车通过这段公路最少需要$\frac{1}{2}$h。

答案： $\frac{1}{2}$