《2025年春如金卷课时作业AB本九年级数学上册北师大版》

9. 深圳市某中学组织学生开展了“青春心向党,红色永传承”党史知识竞赛,为了解学生对党史的掌握情况,该校随机抽取了部分学生的竞赛成绩,将成绩分为A,B,C,D四个等级,并绘制成如图所示的两幅不完整的统计图:

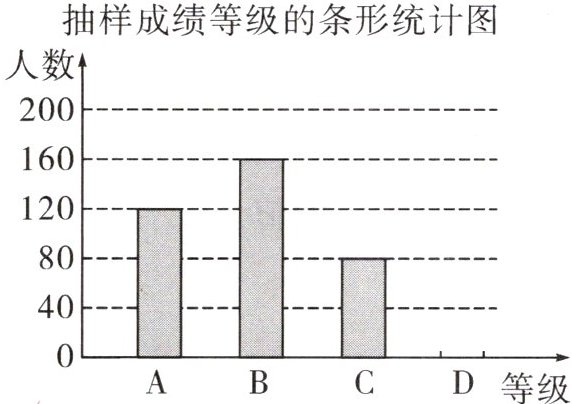
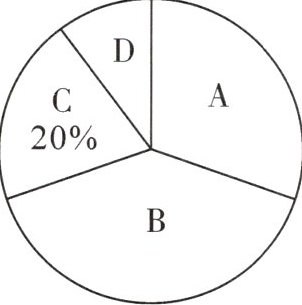
(1)本次共抽取了____名学生的竞赛成绩,并补全条形统计图;
(2)若该校共有2000人参加本次竞赛活动,估计竞赛成绩为B等级的学生人数为____人;
(3)学校在竞赛成绩为A等级中的甲、乙、丙、丁这4名学生里,随机选取2人参加学校党史报告活动,用画树状图或列表法求出甲、乙两人同时被选中的概率。

答案：
9.解:
(1)本次共抽取了$80÷20\%=400$名学生的竞赛成绩。
D等级的人数为$400-120-160-80=40$人。
补全条形统计图如图所示。
　　　　　抽样成绩等级的条形统计图
　　　
故答案为:400。
(2)$2000×\frac{160}{400}=800$人。
∴估计竞赛成绩为B等级的学生人数约为800人。
故答案为:800。
(3)列表如下:
　　　甲　　　　乙　　　　丙　　　　丁
　　　甲　　　　　　　　(甲,乙)　(甲，丙)　(甲，丁)
　　　乙　　(乙，甲)(乙,丙)(乙,丁)
　　　丙　　(丙，甲)(丙，乙)(丙，丁)
　　　丁　　(丁，甲)(丁，乙)(丁，丙)
共有12种等可能的结果，其中甲、乙两人同时被选中的结果有:(甲，乙)，(乙，甲)，共2种，
∴甲、乙两人同时被选中的概率为$\frac{2}{12}=\frac{1}{6}$。

10. 一款游戏的规则如下:如图1为游戏棋盘,从起点到终点共7步;如图2是一个被分成4个大小相等的扇形的转盘,转动转盘,待转盘自动停止后,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止),每次棋子按照指针所指的数字前进相应的步数,若棋子最终能恰好落在终点的视为通过游戏。

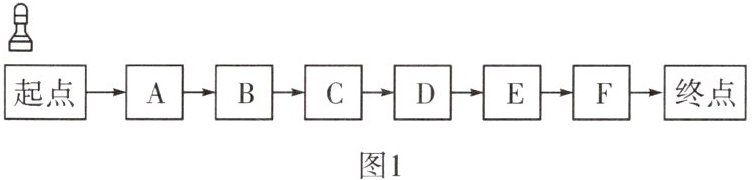
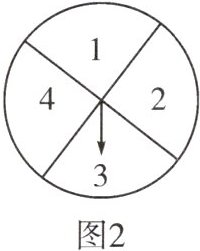
(1)转动转盘一次,求转盘停止后指针指向4的概率($\frac{1}{4}$);
(2)请用列表或画树状图法,求转动转盘两次能通过游戏的概率($\frac{1}{8}$)。

答案： 10.
(1)
∵转盘被分成4个大小相等的扇形，
∴$P$(指针指向4)$=\frac{1}{4}$。
(2)列表如下:
　　　1　　　　2　　　　3　　　　4
　　　1　　　　　2　　　　3　　　　4　　　　5
　　　2　　　　3　　　　4　　　　5　　　　6
　　　3　　　　4　　　　5　　　　6　　　　7
　　　4　　　　5　　　　6　　　　7　　　　8
通过游戏是恰好到达终点即两次指针所指扇形区域数字之和为7，由表可得共有16种等可能的结果，其中和为7的结果有2种，
∴$P$(转动转盘两次能通过游戏)$=\frac{2}{16}=\frac{1}{8}$。