A. 如图,在菱形ABCD中,对角线AC,BD相交于点O。
(1)若$∠ADC=50^{\circ }$,则$∠ADB=$
(2)若$BD=8$,$AC=6$,则$AD=$
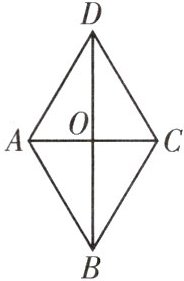
(1)若$∠ADC=50^{\circ }$,则$∠ADB=$
25
$^{\circ }$;(2)若$BD=8$,$AC=6$,则$AD=$
5
,$AB=$5
,$∠AOD=$90
$^{\circ }$,菱形ABCD的面积=24
。
答案:
(1)25
(2)5 5 90 24
(1)25
(2)5 5 90 24
B. 如图,在菱形ABCD中,对角线$AC=4$,$∠BAD=120^{\circ }$,则菱形ABCD的周长为 (
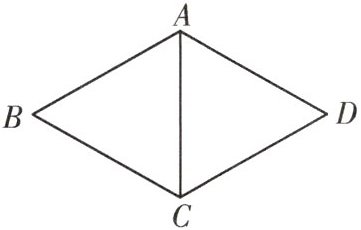
A.20
B.18
C.16
D.15
C
)
A.20
B.18
C.16
D.15
答案:
C
解析:由题意知$\triangle ABC$是等边三角形,$\therefore AB=AC=4$,$C_{菱形ABCD}=4AB=16$,故选C。
解析:由题意知$\triangle ABC$是等边三角形,$\therefore AB=AC=4$,$C_{菱形ABCD}=4AB=16$,故选C。
C. 如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E,求证:$DE=AC$。
证明:$\because$四边形ABCD是菱形,
$\therefore AB// CD$,$AC\perp BD$,
$\therefore AE// CD$,$∠AOB=90^{\circ }$。
$\because DE\perp BD$,即$∠EDB=90^{\circ }$,
$\therefore$
$\therefore DE// AC$,
$\therefore$四边形ACDE是平行四边形,
$\therefore$
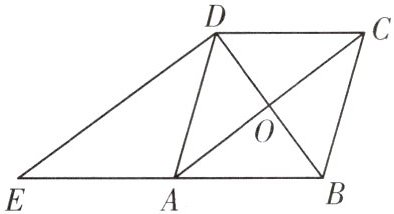
证明:$\because$四边形ABCD是菱形,
$\therefore AB// CD$,$AC\perp BD$,
$\therefore AE// CD$,$∠AOB=90^{\circ }$。
$\because DE\perp BD$,即$∠EDB=90^{\circ }$,
$\therefore$
$∠AOB=∠EDB$
,$\therefore DE// AC$,
$\therefore$四边形ACDE是平行四边形,
$\therefore$
$DE=AC$
。
答案:
$∠AOB=∠EDB$;$DE=AC$
1. 如图,在菱形ABCD中,对角线AC,BD相交于点O。
(1)若$∠ADC=70^{\circ }$,则$∠ADB=$
(2)若$BD=16$,$AC=12$,则$AD=$
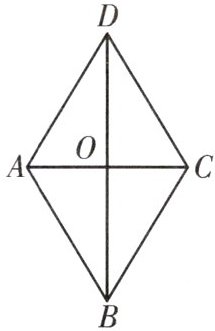
(1)若$∠ADC=70^{\circ }$,则$∠ADB=$
35
$^{\circ }$;(2)若$BD=16$,$AC=12$,则$AD=$
10
,$AB=$10
,$∠BOC=$90
$^{\circ }$,菱形ABCD的周长=40
。
答案:
(1)35
(2)10 10 90 40
(1)35
(2)10 10 90 40
2. 如图,菱形ABCD的两条对角线相交于点O,若$AC=6$,菱形的面积等于12,则菱形ABCD的周长等于 (
A. 4
B. $2\sqrt {3}$
C. $\sqrt {13}$
D. $4\sqrt {13}$
D
)
A. 4
B. $2\sqrt {3}$
C. $\sqrt {13}$
D. $4\sqrt {13}$
答案:
D
3. 如图,在菱形ABCD中,过点B作$BE\perp AD$,垂足为E,过点B作$BF\perp CD$,垂足为F。求证:$AE=CF$。
证明:∵四边形ABCD是菱形,
∴
∵BE⊥AD,BF⊥CD,
∴
在△ABE与△CBF中,$\left\{\begin{array}{l} ∠BEA=∠BFC=90^{\circ },\\ ∠A=∠C,\\ BA=BC,\end{array}\right.$
∴
∴AE=CF。
证明:∵四边形ABCD是菱形,
∴
BA=BC,∠A=∠C
。∵BE⊥AD,BF⊥CD,
∴
∠BEA=∠BFC=90°
。在△ABE与△CBF中,$\left\{\begin{array}{l} ∠BEA=∠BFC=90^{\circ },\\ ∠A=∠C,\\ BA=BC,\end{array}\right.$
∴
△ABE≌△CBF(AAS)
,∴AE=CF。
答案:
证明:
∵四边形ABCD是菱形,
∴BA=BC,∠A=∠C。
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°。
在△ABE与△CBF中,$\left\{\begin{array}{l} ∠BEA=∠BFC=90^{\circ },\\ ∠A=∠C,\\ BA=BC,\end{array}\right.$
∴△ABE≌△CBF(AAS),
∴AE=CF。
∵四边形ABCD是菱形,
∴BA=BC,∠A=∠C。
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°。
在△ABE与△CBF中,$\left\{\begin{array}{l} ∠BEA=∠BFC=90^{\circ },\\ ∠A=∠C,\\ BA=BC,\end{array}\right.$
∴△ABE≌△CBF(AAS),
∴AE=CF。
查看更多完整答案,请扫码查看


