《2025年春如金卷课时作业AB本九年级数学上册北师大版》

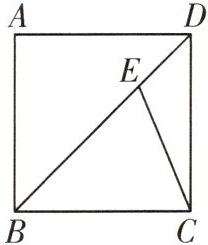
A. 如图，在正方形ABCD中，E是对角线BD上的一点，且BE=AB，连接CE。若AB=2，则△CBE的面积为$\sqrt{2}$。

答案： $\sqrt{2}$

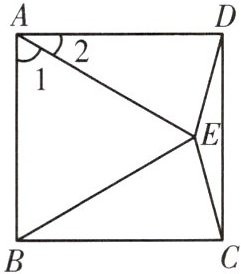
B. 如图，点E是正方形ABCD内一点，如果△ABE为等边三角形，求∠EDC的度数。
解：∵△ABE为等边三角形，
∴∠1=60°，AB=AE。
又∵四边形ABCD为正方形，
∴∠BAD=90°，AB=AD，
∴∠2=30°，AD=AE，
∴∠ADE=75°，
∴∠EDC=90°−∠ADE=90°−75°=15°。

答案： 四边形ABCD为正方形；∠EDC=90°−∠ADE=90°−75°=15°

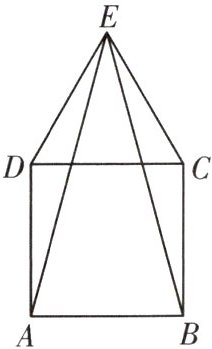
C. 如图，正方形ABCD及等边三角形EDC按如图位置放置，连接AE，BE。求证：AE=BE。
证明：由正方形ABCD以及等边三角形EDC的性质可知：
AD=BC，ED=EC，
∠ADC=∠BCD=90°，
∠EDC=∠ECD=60°，
∴∠ADE=∠ADC+∠EDC=150°，∠BCE=∠BCD+∠ECD=150°，
∴∠ADE=∠BCE。
在△ADE与△BCE中，$\left\{\begin{array}{l}ED=EC,\\ \angle EDA=\angle BCE,\\ AD=BC,\end{array}\right.$
∴△ADE≌△BCE(SAS)，
∴AE=BE。

答案： ∠ADE=∠BCE；AE=BE

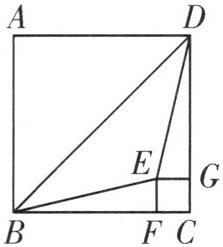
1. 如图，四边形ABCD与四边形EFCG都是正方形，若AB=5，$S_{\triangle BED}=10$，则DG=$\frac{9}{2}$。

答案： $\frac{9}{2}$

2. 如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，求∠BCE的度数。

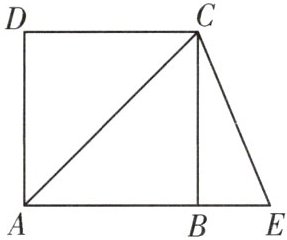
解：∵四边形$ABCD$是正方形，
∴$∠BAC=∠ACB=$45°。
∵$AE=AC$，
∴$∠ACE=∠E=$$\frac{180^{\circ}-45^{\circ}}{2}=67.5^{\circ}$，
∴$∠BCE=∠ACE - ∠ACB=$$67.5^{\circ}-45^{\circ}=22.5^{\circ}$。

答案： 解：
∵四边形$ABCD$是正方形，
∴$∠BAC=∠ACB=45^{\circ}$。
∵$AE=AC$，
∴$∠ACE=∠E=\frac{180^{\circ}-45^{\circ}}{2}=67.5^{\circ}$，
∴$∠BCE=∠ACE - ∠ACB=67.5^{\circ}-45^{\circ}=22.5^{\circ}$。

3. 如图，E为正方形ABCD的边BC延长线上的点，F是CD边上一点，且CE=CF，连接DE，BF。求证：DE=BF。
证明：∵四边形ABCD是正方形，
∴BC=DC，∠BCD=90°。
∵E为BC延长线上的点，
∴∠DCE=90°，
∴∠BCD=∠DCE。
在△BCF和△DCE中，$\left\{\begin{array}{l} BC=DC,\\ ∠BCD=∠DCE,\\ CF=CE,\end{array}\right.$
∴△BCF≌△DCESAS，
∴DE=BF。

答案： 证明：
∵四边形$ABCD$是正方形，
∴$BC=DC$，$∠BCD=90^{\circ}$。
∵$E$为$BC$延长线上的点，
∴$∠DCE=90^{\circ}$，
∴$∠BCD=∠DCE$。
在$\triangle BCF$和$\triangle DCE$中，$\left\{\begin{array}{l} BC=DC,\\ ∠BCD=∠DCE,\\ CF=CE,\end{array}\right.$
∴$\triangle BCF≌\triangle DCE(SAS)$，
∴$DE=BF$。