《2025年春如金卷课时作业AB本九年级数学上册北师大版》

10. 某商场将进价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个，但售价不能超过70元。为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少元？

答案： 解：设这种台灯的售价应定为$ x $元，则平均每月可售出$ [ 600 - 10 ( x - 40 ) ] $个，
根据题意得$ ( x - 30 ) [ 600 - 10 ( x - 40 ) ] = 10000 $，
整理得$ x ^ { 2 } - 130 x + 4000 = 0 $，
解得$ x _ { 1 } = 50 $，$ x _ { 2 } = 80 $（舍去）。
答：这种台灯的售价应定为$ 50 $元。

11. 已知关于x的方程$ x^{2}-(k+2)x+2k=0 $。
（1）求证：k取任何实数值，方程总有实数根；
（2）若Rt△ABC的斜边长$ a=3 $，另两边长b，c恰好是这个方程的两个根，求△ABC的周长。
（1）证明：$ \because \Delta = ( k + 2 ) ^ { 2 } - 8 k $
$ = k ^ { 2 } + 4 k + 4 - 8 k $
$ = ( k - 2 ) ^ { 2 } \geqslant 0 $，
$ \therefore $无论$ k $取何值，方程总有实数根。
（2）解：$ \because $边长$ b $，$ c $恰好是方程$ x ^ { 2 } - ( k + 2 ) x + 2 k = 0 $的两个根，
$ \therefore b + c = k + 2 $，$ b c = 2 k $，$ ( k ＞ 0 ) $，
$ \because \mathrm { Rt } \triangle A B C $的斜边长$ a = 3 $，
$ \therefore b ^ { 2 } + c ^ { 2 } = 3 ^ { 2 } = 9 $，
$ \therefore ( b + c ) ^ { 2 } - 2 b c = 9 $，即$ ( k + 2 ) ^ { 2 } - 2 × 2 k = 9 $，解得$ k = \pm \sqrt { 5 } $（负值舍去），
$ \therefore b + c = \sqrt { 5 } + 2 $，
$ \therefore \triangle A B C $的周长为$ a + b + c = 3 + \sqrt { 5 } + 2 = $$ 5 + \sqrt { 5 } $。

答案：
(1)证明：$ \because \Delta = ( k + 2 ) ^ { 2 } - 8 k $
$ = k ^ { 2 } + 4 k + 4 - 8 k $
$ = ( k - 2 ) ^ { 2 } \geqslant 0 $，
$ \therefore $无论$ k $取何值，方程总有实数根。
(2)解：$ \because $边长$ b $，$ c $恰好是方程$ x ^ { 2 } - ( k + 2 ) x + 2 k = 0 $的两个根，
$ \therefore b + c = k + 2 $，$ b c = 2 k $，$ ( k ＞ 0 ) $，
$ \because \mathrm { Rt } \triangle A B C $的斜边长$ a = 3 $，
$ \therefore b ^ { 2 } + c ^ { 2 } = 3 ^ { 2 } = 9 $，
$ \therefore ( b + c ) ^ { 2 } - 2 b c = 9 $，即$ ( k + 2 ) ^ { 2 } - 2 \times 2 k = 9 $，解得$ k = \pm \sqrt { 5 } $（负值舍去），
$ \therefore b + c = \sqrt { 5 } + 2 $，
$ \therefore \triangle A B C $的周长为$ a + b + c = 3 + \sqrt { 5 } + 2 = 5 + \sqrt { 5 } $。

12. 已知关于x的一元二次方程$ x^{2}+2(m-1)x+m^{2}=0 $。
（1）若方程有实数根，求m的取值范围；
（2）若方程的两实数根分别为$ x_{1} $，$ x_{2} $，且满足$ x_{1}^{2}+x_{2}^{2}=14 $。求$ x_{1}^{2}+4x_{2}-10 $的值。
（1）$ m \leqslant \frac { 1 } { 2 } $
（2）5

答案： 解：
(1)$ \because $关于$ x $的一元二次方程$ x ^ { 2 } + 2 ( m - 1 ) x + m ^ { 2 } = 0 $有实数根，
$ \therefore \Delta = b ^ { 2 } - 4 a c = [ 2 ( m - 1 ) ] ^ { 2 } - 4 \times 1 \times m ^ { 2 } \geqslant 0 $，
解得：$ m \leqslant \frac { 1 } { 2 } $，
$ \therefore $实数$ m $的取值范围为$ m \leqslant \frac { 1 } { 2 } $。
(2)$ \because x _ { 1 } $，$ x _ { 2 } $是关于$ x $的一元二次方程$ x ^ { 2 } + 2 ( m - 1 ) x + m ^ { 2 } = 0 $的两实数根，
$ \therefore x _ { 1 } + x _ { 2 } = - 2 ( m - 1 ) $，$ x _ { 1 } \cdot x _ { 2 } = m ^ { 2 } $。
$ \because x _ { 1 } ^ { 2 } + x _ { 2 } ^ { 2 } = 14 $，
$ \therefore ( x _ { 1 } + x _ { 2 } ) ^ { 2 } - 2 x _ { 1 } \cdot x _ { 2 } = 14 $，
$ \therefore [ - 2 ( m - 1 ) ] ^ { 2 } - 2 m ^ { 2 } = 14 $，
$ \therefore 4 m ^ { 2 } - 8 m + 4 - 2 m ^ { 2 } = 14 $，
$ \therefore m = 5 $或$ - 1 $，
当$ m = 5 $时，方程$ x ^ { 2 } + 2 ( m - 1 ) x + m ^ { 2 } = 0 $变为$ x ^ { 2 } + 8 x + 25 = 0 $，无解舍去，
当$ m = - 1 $时，方程变为$ x ^ { 2 } - 4 x + 1 = 0 $，
$ \therefore x _ { 1 } + x _ { 2 } = 4 $，$ x _ { 1 } ^ { 2 } - 4 x _ { 1 } + 1 = 0 $，
$ \therefore x _ { 1 } ^ { 2 } = 4 x _ { 1 } - 1 $，
$ \therefore x _ { 1 } ^ { 2 } + 4 x _ { 2 } - 10 = 4 x _ { 1 } - 1 + 4 x _ { 2 } - 10 = 4 ( x _ { 1 } + x _ { 2 } ) - 11 = 16 - 11 = 5 $。

13. 如图，在△ABC中，$ ∠C=90^{\circ} $，$ AC=4cm $，$ BC=3cm $，动点D从点A出发以4cm/s的速度向点C运动，同时动点E从C出发以3cm/s的速度向点B运动，设它们的运动时间为t s。
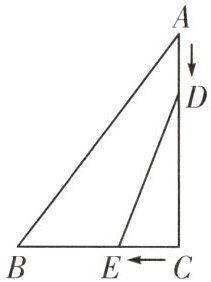
（1）根据题意知：$ CE= $$ 3 t \mathrm { cm } $，$ CD= $________$ ( 4 - 4 t ) \mathrm { cm } $；（用含t的代数式表示）
（2）t为何值时，△CDE的面积等于四边形ABED的面积的$ \frac{1}{3} $？
（3）在运动过程中（不含端点），DE的长可以是4cm吗？如果可以，请求出t的值；如果不可以，请说明理由。

答案： 解：
(1)$ 3 t \mathrm { cm } $，$ ( 4 - 4 t ) \mathrm { cm } $。
(2)$ \because \triangle C D E $的面积等于四边形$ A B E D $的面积的$ \frac { 1 } { 3 } $，
$ \therefore \triangle C D E $的面积等于三角形$ A B C $的面积的$ \frac { 1 } { 4 } $，
$ \therefore \frac { 1 } { 2 } C E \cdot C D = \frac { 1 } { 4 } \times \frac { 1 } { 2 } A C \cdot B C $，
即$ \frac { 1 } { 2 } \times 3 t \times ( 4 - 4 t ) = \frac { 1 } { 4 } \times \frac { 1 } { 2 } \times 4 \times 3 $，
化简得$ 4 t ^ { 2 } - 4 t + 1 = 0 $，
解得$ t _ { 1 } = t _ { 2 } = \frac { 1 } { 2 } $，
即当$ t $为$ \frac { 1 } { 2 } $时，$ \triangle C D E $的面积等于四边形$ A B E D $的面积的$ \frac { 1 } { 3 } $。
(3)不可以，理由如下：若$ D E = 4 \mathrm { cm } $，由勾股定理得$ 4 ^ { 2 } = ( 3 t ) ^ { 2 } + ( 4 - 4 t ) ^ { 2 } $，
整理得$ 25 t ^ { 2 } - 32 t = 0 $，
解得$ t _ { 1 } = \frac { 32 } { 25 } $，$ t _ { 2 } = 0 $（舍去），
当$ t = \frac { 32 } { 25 } $时，$ C E = 3 t = \frac { 96 } { 25 } ＞ B C $，不合题意，
$ \therefore D E $的长不可以是$ 4 \mathrm { cm } $。