4. 下列图形中一定是相似形的是(
A. 两个等边三角形
B. 两个菱形
C. 两个矩形
D. 两个直角三角形
A
)A. 两个等边三角形
B. 两个菱形
C. 两个矩形
D. 两个直角三角形
答案:
A
5. 下列说法中,正确的是(
A. 两个矩形必相似
B. 两个含 $45^{\circ}$ 角的等腰三角形必相似
C. 两个含 $30^{\circ}$ 角的直角三角形必相似
D. 两个菱形必相似
C
)A. 两个矩形必相似
B. 两个含 $45^{\circ}$ 角的等腰三角形必相似
C. 两个含 $30^{\circ}$ 角的直角三角形必相似
D. 两个菱形必相似
答案:
C
6. 小康利用复印机将一张长为 $5\mathrm{cm}$,周长为 $16\mathrm{cm}$ 的矩形图片放大,其中放大后的矩形长为 $10\mathrm{cm}$,则放大后的矩形周长为(
A. $16\mathrm{cm}$
B. $21\mathrm{cm}$
C. $32\mathrm{cm}$
D. $42\mathrm{cm}$
C
)A. $16\mathrm{cm}$
B. $21\mathrm{cm}$
C. $32\mathrm{cm}$
D. $42\mathrm{cm}$
答案:
C
7. 如图,两个菱形,两个等边三角形,两个等腰直角三角形,两个矩形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,则两个图形对应边不成比例的一组是(
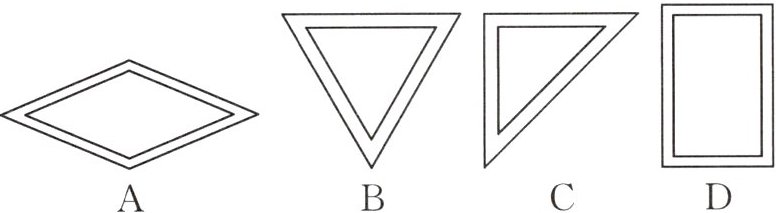
D
)
答案:
D
8. 如图,图中的这两个五边形相似,根据图中标注数据求 $a$,$b$,$c$ 的值以及 $\angle \alpha$ 和 $\angle \beta$ 的度数。
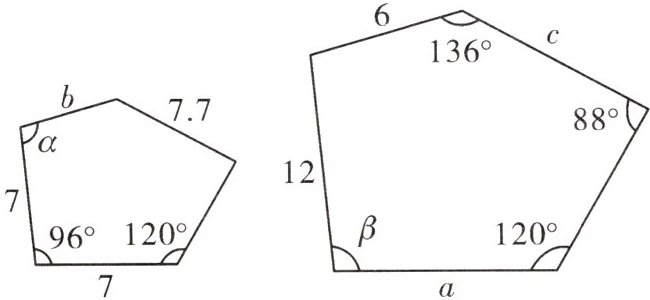
$a=$

$a=$
12
,$b=$3.5
,$c=$13.2
,$\angle \alpha=$100°
,$\angle \beta=$96°
。
答案:
$a = 12$,$b = 3.5$,$c = 13.2$,$\angle \beta = 96^{\circ}$,$\angle \alpha = 100^{\circ}$。
9. 如图,取一张长为 $a$,宽为 $b$ 的矩形纸片,将它对折两次后得到一张小矩形纸片,若要使小矩形与原矩形相似,则原矩形纸片的边 $a$,$b$ 应满足的条件是(
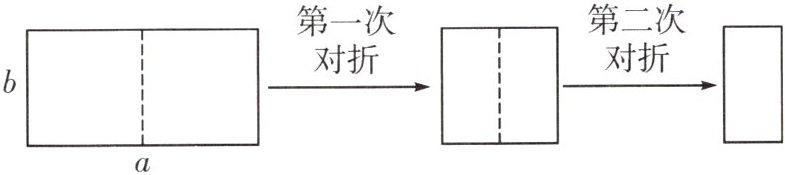
A. $a = 2\sqrt{2}b$
B. $a = \sqrt{2}b$
C. $a = 4b$
D. $a = 2b$
D
)
A. $a = 2\sqrt{2}b$
B. $a = \sqrt{2}b$
C. $a = 4b$
D. $a = 2b$
答案:
D
10. 如图在矩形 $ABCD$ 中,$AB = 12$,$BC = 16$,$E$,$F$ 分别是 $AB$,$CD$ 上的点,且 $AE = DF = 8$,两动点 $M$,$N$ 都以 $2\mathrm{cm/s}$ 的速度分别从 $C$,$F$ 两点沿 $CB$,$FE$ 向 $B$,$E$ 两点运动,判断当 $M$,$N$ 运动多长时间能使矩形 $CFNM$ 与矩形 $AEFD$ 相似,并证明你的结论。
解:设运动 $t\mathrm{s}$ 能使矩形 $CFNM$ 与矩形 $AEFD$ 相似,由题意,得 $\frac{AD}{NF}=\frac{DF}{FC}$ 即 $\frac{16}{2t}=\frac{8}{12 - 8}$ 或 $\frac{AD}{FC}=\frac{DF}{NF}$ 即 $\frac{16}{12 - 8}=\frac{8}{2t}$,解得 $t =$
解:设运动 $t\mathrm{s}$ 能使矩形 $CFNM$ 与矩形 $AEFD$ 相似,由题意,得 $\frac{AD}{NF}=\frac{DF}{FC}$ 即 $\frac{16}{2t}=\frac{8}{12 - 8}$ 或 $\frac{AD}{FC}=\frac{DF}{NF}$ 即 $\frac{16}{12 - 8}=\frac{8}{2t}$,解得 $t =$
4
或1
。当 $t = 4$ 时,$NF = 8$,∵$\frac{AD}{NF}=\frac{DF}{FC}=\frac{2}{1}$,∵$CFNM$ 与 $AEFD$ 都是矩形,∴矩形 $CFNM$ 与矩形 $AEFD$ 相似。同理可证当 $t = 1$ 时矩形 $CFNM$ 与矩形 $AEFD$ 相似。
答案:
解:设运动 $t\mathrm{s}$ 能使矩形 $CFNM$ 与矩形 $AEFD$ 相似,由题意,得 $\frac{AD}{NF}=\frac{DF}{FC}$ 即 $\frac{16}{2t}=\frac{8}{12 - 8}$ 或 $\frac{AD}{FC}=\frac{DF}{NF}$ 即 $\frac{16}{12 - 8}=\frac{8}{2t}$,解得 $t = 4$ 或 $1$。当 $t = 4$ 时,$NF = 8$,
∵$\frac{AD}{NF}=\frac{DF}{FC}=\frac{2}{1}$,
∵$CFNM$ 与 $AEFD$ 都是矩形,
∴矩形 $CFNM$ 与矩形 $AEFD$ 相似。同理可证当 $t = 1$ 时矩形 $CFNM$ 与矩形 $AEFD$ 相似。
∵$\frac{AD}{NF}=\frac{DF}{FC}=\frac{2}{1}$,
∵$CFNM$ 与 $AEFD$ 都是矩形,
∴矩形 $CFNM$ 与矩形 $AEFD$ 相似。同理可证当 $t = 1$ 时矩形 $CFNM$ 与矩形 $AEFD$ 相似。
查看更多完整答案,请扫码查看


