《2025年春如金卷课时作业AB本九年级数学上册北师大版》

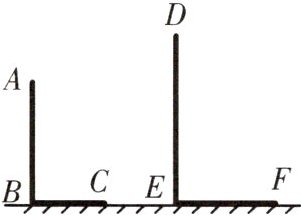
12. 如图,$AB$和$DE$是直立在地面上的两根立柱,$AB=6m$,$AB$在阳光下的影长$BC=3m$,在同一时刻阳光下$DE$的影长$EF=4m$,则$DE$的长为 (C)

A. $4m$
B. $6m$
C. $8m$
D. $10m$

答案： C

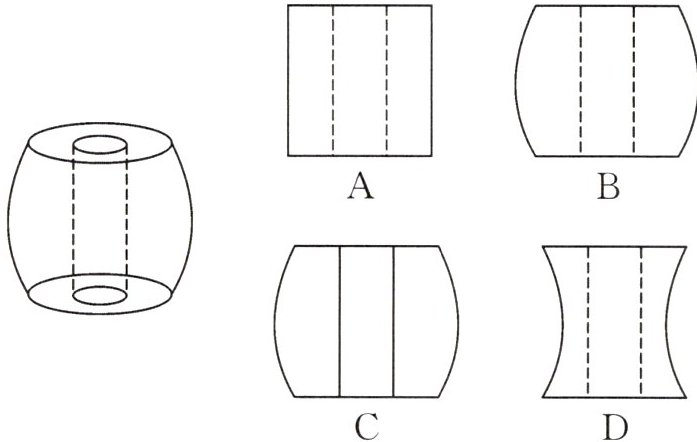
13. 如图所示是一个放在水平面上的几何体,它的主视图是 (B)

答案： B

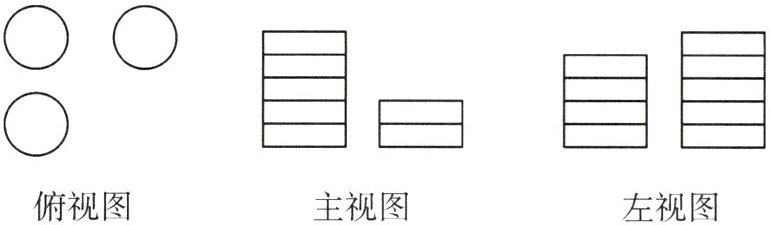
14. 桌子上重叠摆放了若干枚面值为1元的硬币,它的三种视图如图所示,则桌上共有1元硬币的数量为 (B)

A. 12枚
B. 11枚
C. 9枚
D. 7枚

答案： B

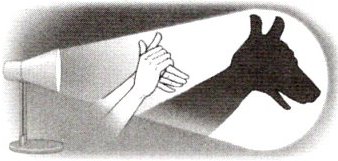
15. 手影游戏利用的物理原理是:光是沿直线传播的。图中小狗手影就是我们小时候常玩的游戏,在一次游戏中,小明距离墙壁$1m$,爸爸拿着的光源与小明的距离为$2m$,在小明不动的情况下,要使小狗手影的高度增加一倍,则光源与小明的距离应 (A)

A. 减少$\frac {3}{2}m$
B. 增加$\frac {3}{2}m$
C. 减少$\frac {5}{3}m$
D. 增加$\frac {5}{3}m$

答案： A

16. 由几个相同的边长为1的小正方体搭成的几何体的俯视图如图所示,方格中的数字表示该位置的小正方体的个数。请在下面方格纸中分别画出这个几何体的主视图和左视图。

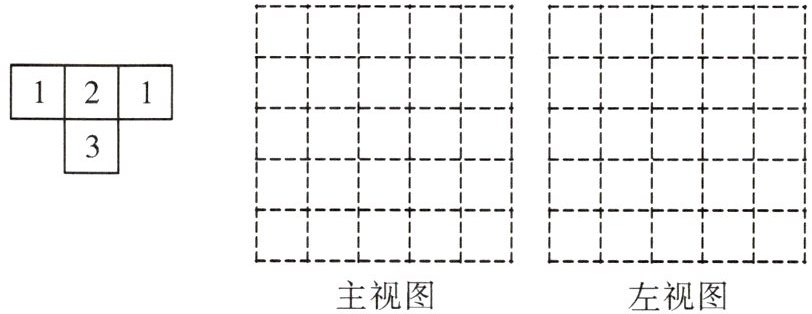
答案：
解:如图所示:
　　　　

17. 如图,在$A$时测得某树的影长为$4m$,$B$时又测得该树的影长为$16m$,若两次日照的光线互相垂直,求树的高度。

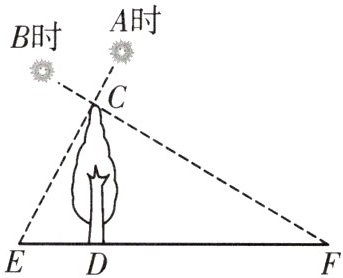
答案：
解:如图,过点C作CD⊥EF,垂足为点D,由题意得:△EFC是直角三角形,∠ECF = 90°,
∴∠EDC = ∠CDF = 90°,
∴∠E + ∠ECD = ∠ECD + ∠DCF = 90°,
∴∠E = ∠DCF,
∴Rt△EDC∽Rt△CDF,
∴$\frac{ED}{DC}$ = $\frac{DC}{FD}$,即$DC^2$ = $ED \cdot FD$。
　代入数据可得$DC^2$ = 64,
∴DC = 8m。故树的高度为8m。