4. 正方形具有而菱形不一定具有的性质是(
A. 对角线相等
B. 四条边相等
C. 对角线互相垂直
D. 每条对角线平分一组对角
A
)A. 对角线相等
B. 四条边相等
C. 对角线互相垂直
D. 每条对角线平分一组对角
答案:
A
5. 正方形具有而矩形不具有的性质是(
A. 对角线互相垂直
B. 对角相等
C. 对角线互相平分
D. 四角相等
A
)A. 对角线互相垂直
B. 对角相等
C. 对角线互相平分
D. 四角相等
答案:
A
6. 如图,以正方形ABCD的边AB为一边向外作等边三角形ABE,则∠AED的度数为(
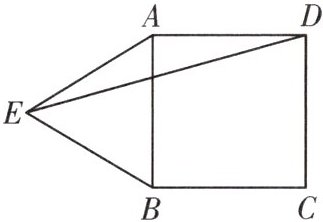
A. 15°
B. 20°
C. 22.5°
D. 25°
A
)
A. 15°
B. 20°
C. 22.5°
D. 25°
答案:
A
7. 如果一个正方形的对角线长为$\sqrt{3}$,那么它的面积为
$\frac{3}{2}$
。
答案:
$\frac{3}{2}$
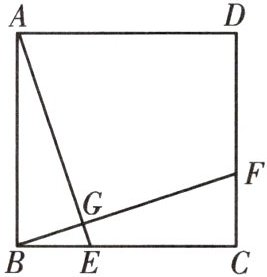
8. 如图,点E,F在正方形ABCD的边BC,CD上,AE,BF相交于点G,BE=CF。
(1)求证:AE=BF;
证明:∵四边形$ABCD$是正方形,
∴$AB=BC$,$∠ABE=∠BCF=90^{\circ}$。
又∵$BE=CF$,
∴$\triangle ABE≌\triangle BCF(SAS)$,
∴$AE=BF$。
(2)求证:AE⊥BF。
证明:由(1)知$∠BAE=∠CBF$。
∵$∠BAE+∠AEB=90^{\circ}$,
∴$∠CBF+∠AEB=90^{\circ}$,
∴$∠BGE=90^{\circ}$,即$AE⊥BF$。
(1)求证:AE=BF;
证明:∵四边形$ABCD$是正方形,
∴$AB=BC$,$∠ABE=∠BCF=90^{\circ}$。
又∵$BE=CF$,
∴$\triangle ABE≌\triangle BCF(SAS)$,
∴$AE=BF$。
(2)求证:AE⊥BF。
证明:由(1)知$∠BAE=∠CBF$。
∵$∠BAE+∠AEB=90^{\circ}$,
∴$∠CBF+∠AEB=90^{\circ}$,
∴$∠BGE=90^{\circ}$,即$AE⊥BF$。

答案:
(1)证明:
∵四边形$ABCD$是正方形,
∴$AB=BC$,$∠ABE=∠BCF=90^{\circ}$。
又
∵$BE=CF$,
∴$\triangle ABE≌\triangle BCF(SAS)$,
∴$AE=BF$。
(2)证明:由
(1)知$∠BAE=∠CBF$。
∵$∠BAE+∠AEB=90^{\circ}$,
∴$∠CBF+∠AEB=90^{\circ}$,
∴$∠BGE=90^{\circ}$,即$AE⊥BF$。
(1)证明:
∵四边形$ABCD$是正方形,
∴$AB=BC$,$∠ABE=∠BCF=90^{\circ}$。
又
∵$BE=CF$,
∴$\triangle ABE≌\triangle BCF(SAS)$,
∴$AE=BF$。
(2)证明:由
(1)知$∠BAE=∠CBF$。
∵$∠BAE+∠AEB=90^{\circ}$,
∴$∠CBF+∠AEB=90^{\circ}$,
∴$∠BGE=90^{\circ}$,即$AE⊥BF$。
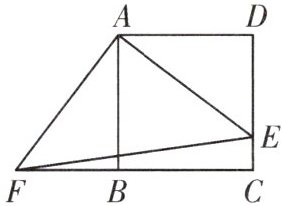
9. 如图,四边形ABCD是正方形,E,F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF。
(1)求证:△ADE≌△ABF;
(2)若BC=4,CE=1,求△AEF的面积。
(1)证明:∵四边形$ABCD$是正方形,
∴$AB=AD=BC=CD$,$∠BAD=∠ABC=∠ADE=90^{\circ}$,
∴$∠ABF=90^{\circ}=∠ADE$。
∵$AB=AD$,$∠ABF=∠ADE$,$BF=DE$,
∴$\triangle ADE≌\triangle ABF$(
(2)解:∵$BC=4$,$CE=1$,
∴$AD=4$,$DE=3$,
由勾股定理,得$AE^{2}=AD^{2}+DE^{2}=25$。
∵$\triangle ADE≌\triangle ABF$,
∴$AF=AE$,$∠BAF=∠DAE$,
∴$∠BAF+∠BAE=∠DAE+∠BAE=90^{\circ}$,
即$∠EAF=90^{\circ}$,
∴$S_{\triangle AEF}=\frac{1}{2}AE×AF=\frac{1}{2}AE^{2}=$
∴$\triangle AEF$的面积为
(1)求证:△ADE≌△ABF;
(2)若BC=4,CE=1,求△AEF的面积。

(1)证明:∵四边形$ABCD$是正方形,
∴$AB=AD=BC=CD$,$∠BAD=∠ABC=∠ADE=90^{\circ}$,
∴$∠ABF=90^{\circ}=∠ADE$。
∵$AB=AD$,$∠ABF=∠ADE$,$BF=DE$,
∴$\triangle ADE≌\triangle ABF$(
SAS
);(2)解:∵$BC=4$,$CE=1$,
∴$AD=4$,$DE=3$,
由勾股定理,得$AE^{2}=AD^{2}+DE^{2}=25$。
∵$\triangle ADE≌\triangle ABF$,
∴$AF=AE$,$∠BAF=∠DAE$,
∴$∠BAF+∠BAE=∠DAE+∠BAE=90^{\circ}$,
即$∠EAF=90^{\circ}$,
∴$S_{\triangle AEF}=\frac{1}{2}AE×AF=\frac{1}{2}AE^{2}=$
$\frac{25}{2}$
,∴$\triangle AEF$的面积为
$\frac{25}{2}$
。
答案:
(1)证明:
∵四边形$ABCD$是正方形,
∴$AB=AD=BC=CD$,$∠BAD=∠ABC=∠ADE=90^{\circ}$,
∴$∠ABF=90^{\circ}=∠ADE$。
∵$AB=AD$,$∠ABF=∠ADE$,$BF=DE$,
∴$\triangle ADE≌\triangle ABF(SAS)$;
(2)解:
∵$BC=4$,$CE=1$,
∴$AD=4$,$DE=3$,
由勾股定理,得$AE^{2}=AD^{2}+DE^{2}=25$。
∵$\triangle ADE≌\triangle ABF$,
∴$AF=AE$,$∠BAF=∠DAE$,
∴$∠BAF+∠BAE=∠DAE+∠BAE=90^{\circ}$,
即$∠EAF=90^{\circ}$,
∴$S_{\triangle AEF}=\frac{1}{2}AE×AF=\frac{1}{2}AE^{2}=\frac{25}{2}$,
∴$\triangle AEF$的面积为$\frac{25}{2}$。
(1)证明:
∵四边形$ABCD$是正方形,
∴$AB=AD=BC=CD$,$∠BAD=∠ABC=∠ADE=90^{\circ}$,
∴$∠ABF=90^{\circ}=∠ADE$。
∵$AB=AD$,$∠ABF=∠ADE$,$BF=DE$,
∴$\triangle ADE≌\triangle ABF(SAS)$;
(2)解:
∵$BC=4$,$CE=1$,
∴$AD=4$,$DE=3$,
由勾股定理,得$AE^{2}=AD^{2}+DE^{2}=25$。
∵$\triangle ADE≌\triangle ABF$,
∴$AF=AE$,$∠BAF=∠DAE$,
∴$∠BAF+∠BAE=∠DAE+∠BAE=90^{\circ}$,
即$∠EAF=90^{\circ}$,
∴$S_{\triangle AEF}=\frac{1}{2}AE×AF=\frac{1}{2}AE^{2}=\frac{25}{2}$,
∴$\triangle AEF$的面积为$\frac{25}{2}$。
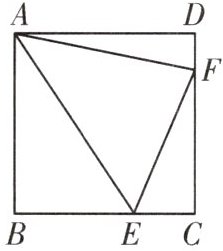
10. 如图,在正方形ABCD中,AB=6,动点E,F分别在边BC,CD上,且∠EAF=45°,连接EF。
(1)求证:EF=BE+DF;
(2)若BE=3,求线段DF的长。
(1)求证:EF=BE+DF;
(2)若BE=3,求线段DF的长。

答案:
(1)证明:如图,延长$CB$到点$G$,使$BG=DF$,连接$AG$。
∵$AD=AB$,$∠ABG=∠ADF =90^{\circ}$ ,
,
∴$\triangle ADF≌\triangle ABG(SAS)$,
∴$AF=AG$,$∠DAF=∠BAG$。
∵四边形$ABCD$为正方形,
∴$∠BAD=90^{\circ}$
∵$∠EAF=45^{\circ}$,
∴$∠BAE+∠DAF=45^{\circ}$,
∴$∠BAG+∠BAE=45^{\circ}=∠EAF$。
在$\triangle AGE$和$\triangle AFE$中,$\left\{\begin{array}{l} AG=AF,\\ ∠GAE=∠EAF,\\ AE=AE,\end{array}\right.$
∴$\triangle AGE≌\triangle AFE(SAS)$,
∴$GE=EF$。
∵$GE=GB+BE=BE+DF$,
∴$EF=BE+DF$。
(2)解:设$DF=a$,则$CF=6 - a$。
∵$BE=3$,$BC=AB=6$,
∴$CE=3$。
∵$EF=BE+DF=3 + a$,
$CE^{2}+CF^{2}=EF^{2}$,
∴$3^{2}+(6 - a)^{2}=(3 + a)^{2}$,解得$a=2$,
∴$DF=2$。
(1)证明:如图,延长$CB$到点$G$,使$BG=DF$,连接$AG$。
∵$AD=AB$,$∠ABG=∠ADF =90^{\circ}$
 ,
,∴$\triangle ADF≌\triangle ABG(SAS)$,
∴$AF=AG$,$∠DAF=∠BAG$。
∵四边形$ABCD$为正方形,
∴$∠BAD=90^{\circ}$
∵$∠EAF=45^{\circ}$,
∴$∠BAE+∠DAF=45^{\circ}$,
∴$∠BAG+∠BAE=45^{\circ}=∠EAF$。
在$\triangle AGE$和$\triangle AFE$中,$\left\{\begin{array}{l} AG=AF,\\ ∠GAE=∠EAF,\\ AE=AE,\end{array}\right.$
∴$\triangle AGE≌\triangle AFE(SAS)$,
∴$GE=EF$。
∵$GE=GB+BE=BE+DF$,
∴$EF=BE+DF$。
(2)解:设$DF=a$,则$CF=6 - a$。
∵$BE=3$,$BC=AB=6$,
∴$CE=3$。
∵$EF=BE+DF=3 + a$,
$CE^{2}+CF^{2}=EF^{2}$,
∴$3^{2}+(6 - a)^{2}=(3 + a)^{2}$,解得$a=2$,
∴$DF=2$。
查看更多完整答案,请扫码查看


