4. 如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为(
A. $y=\frac{10}{x}$
B. $y=\frac{5}{x}$
C. $y=\frac{20}{x}$
D. $y=\frac{x}{20}$
C
)A. $y=\frac{10}{x}$
B. $y=\frac{5}{x}$
C. $y=\frac{20}{x}$
D. $y=\frac{x}{20}$
答案:
C
5. 电路上在电压保持不变的条件下,电流I(A)与电阻$R(\Omega)$成反比例关系,I与R的函数图象如图,I关于R函数解析式是(
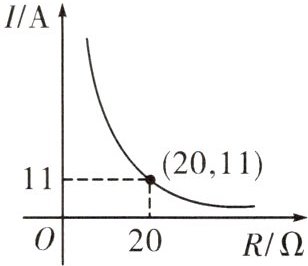
A. $I=\frac{220}{R}$
B. $I=-\frac{220}{R}$
C. $I=\frac{20}{R}$
D. $I=\frac{11}{R}$
A
)
A. $I=\frac{220}{R}$
B. $I=-\frac{220}{R}$
C. $I=\frac{20}{R}$
D. $I=\frac{11}{R}$
答案:
A
6. 实验数据显示,一般成人喝50mL某品牌白酒后,血液中酒精含量y(毫克/百毫升)与时间x(h)变化的图象如图(图象由线段OA与部分双曲线AB组成)所示。国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路。
(1)求部分双曲线AB的函数表达式;
(2)参照上述数学模型,假设某驾驶员晚上22:00在家喝完50毫升该品牌白酒,第二天早上6:30能否驾车去上班?请说明理由。
(1)求部分双曲线AB的函数表达式;
$ y = \frac{180}{x}(x \geq \frac{3}{2}) $
(2)参照上述数学模型,假设某驾驶员晚上22:00在家喝完50毫升该品牌白酒,第二天早上6:30能否驾车去上班?请说明理由。
不能,理由:从晚上22:00到第二天早上6:30时间间距为8.5小时,由$ y = \frac{180}{x} $得当$ y = 20 $时,$ x = 9 $,因为8.5<9,所以第二天早上6:30不能驾车去上班。
答案:
解:
(1)依题意,直线 $ OA $ 过 $ (\frac{1}{4}, 20) $,则直线 $ OA $ 的解析式为 $ y = 80x $,
当 $ x = \frac{3}{2} $ 时,$ y = 120 $,即 $ A(\frac{3}{2}, 120) $,
设双曲线的解析式为 $ y = \frac{k}{x} $,将点 $ A(\frac{3}{2}, 120) $ 代入得:$ k = 180 $,
$ \therefore y = \frac{180}{x}(x \geq \frac{3}{2}) $;
(2)由 $ y = \frac{180}{x} $ 得当 $ y = 20 $ 时,$ x = 9 $,
从晚上 $ 22:00 $ 到第二天早上 $ 6:30 $ 时间间距为 $ 8.5 $ 小时,
$ \because 8.5 < 9 $,
$ \therefore $ 第二天早上 $ 6:30 $ 不能驾车去上班。
(1)依题意,直线 $ OA $ 过 $ (\frac{1}{4}, 20) $,则直线 $ OA $ 的解析式为 $ y = 80x $,
当 $ x = \frac{3}{2} $ 时,$ y = 120 $,即 $ A(\frac{3}{2}, 120) $,
设双曲线的解析式为 $ y = \frac{k}{x} $,将点 $ A(\frac{3}{2}, 120) $ 代入得:$ k = 180 $,
$ \therefore y = \frac{180}{x}(x \geq \frac{3}{2}) $;
(2)由 $ y = \frac{180}{x} $ 得当 $ y = 20 $ 时,$ x = 9 $,
从晚上 $ 22:00 $ 到第二天早上 $ 6:30 $ 时间间距为 $ 8.5 $ 小时,
$ \because 8.5 < 9 $,
$ \therefore $ 第二天早上 $ 6:30 $ 不能驾车去上班。
7. 便民商场出售一批衬衣,衬衣进价为每件80元,在销售中发现,该衬衣的日销售量y(件)是销售单价x(元)的反比例函数,且当销售单价为120元时,每日可销售25件。
(1)求y与x之间的函数解析式;
(2)若商场计划经营此种衬衣的日销售利润为1400元,则销售单价应定为多少元?
(1)求y与x之间的函数解析式;
(2)若商场计划经营此种衬衣的日销售利润为1400元,则销售单价应定为多少元?
答案:
解:
(1)设函数解析式为 $ y = \frac{k}{x}(k \neq 0) $,
$ \because $ 当销售单价为 $ 120 $ 元时,每日可销售 $ 25 $ 件,
$ \therefore 25 = \frac{k}{120} $,解得 $ k = 3000 $,则 $ y $ 与 $ x $ 之间的函数解析式为 $ y = \frac{3000}{x} $。
(2)设单价应定为 $ x $ 元,
$ \because y(x - 80) = 1400 $,
$ \therefore \frac{3000}{x} \cdot (x - 80) = 1400 $,解得 $ x = 150 $,答:销售单价应定为 $ 150 $ 元。
(1)设函数解析式为 $ y = \frac{k}{x}(k \neq 0) $,
$ \because $ 当销售单价为 $ 120 $ 元时,每日可销售 $ 25 $ 件,
$ \therefore 25 = \frac{k}{120} $,解得 $ k = 3000 $,则 $ y $ 与 $ x $ 之间的函数解析式为 $ y = \frac{3000}{x} $。
(2)设单价应定为 $ x $ 元,
$ \because y(x - 80) = 1400 $,
$ \therefore \frac{3000}{x} \cdot (x - 80) = 1400 $,解得 $ x = 150 $,答:销售单价应定为 $ 150 $ 元。
8. 商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡日销售单价x(元)与日销售量y(张)之间有如下关系:
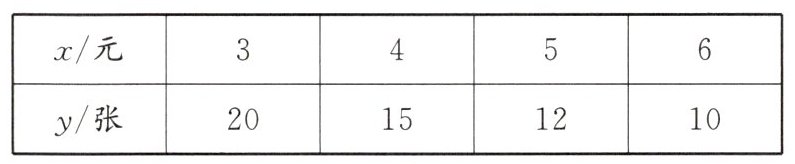
(1)写出y关于x的函数解析式
(2)设经营此贺卡的日销售利润为W(元),试求出W关于x的函数解析式,若物价局规定此贺卡的日销售单价最高不能超过10元/张,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润,并求出最大日销售利润。

(1)写出y关于x的函数解析式
$y = \frac{60}{x}$
;(2)设经营此贺卡的日销售利润为W(元),试求出W关于x的函数解析式,若物价局规定此贺卡的日销售单价最高不能超过10元/张,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润,并求出最大日销售利润。
$W=60 - \frac{120}{x}$;当日销售单价定为10元时,获得最大日销售利润,最大日销售利润为48元。
答案:
解:
(1)设 $ y = \frac{k}{x} $,把 $ x = 3 $,$ y = 20 $ 代入 $ y = \frac{k}{x} $ 得 $ 20 = \frac{k}{3} $,解得 $ k = 60 $,
$ \therefore y = \frac{60}{x} $。
(2)$ w = (x - 2)y = (x - 2) · \frac{60}{x} = 60 - \frac{120}{x} $,
$ \because w $ 随 $ x $ 增大而增大,$ x \leq 10 $,
$ \therefore x = 10 $ 时,$ w = 60 - 12 = 48 $(元)为最大值,
$ \therefore $ 当日销售价为 $ 10 $ 元时,最大日销售利润为 $ 48 $ 元。
(1)设 $ y = \frac{k}{x} $,把 $ x = 3 $,$ y = 20 $ 代入 $ y = \frac{k}{x} $ 得 $ 20 = \frac{k}{3} $,解得 $ k = 60 $,
$ \therefore y = \frac{60}{x} $。
(2)$ w = (x - 2)y = (x - 2) · \frac{60}{x} = 60 - \frac{120}{x} $,
$ \because w $ 随 $ x $ 增大而增大,$ x \leq 10 $,
$ \therefore x = 10 $ 时,$ w = 60 - 12 = 48 $(元)为最大值,
$ \therefore $ 当日销售价为 $ 10 $ 元时,最大日销售利润为 $ 48 $ 元。
查看更多完整答案,请扫码查看


